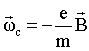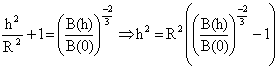Aurélie nov 2001
Ondes hertziennes Capes physique appliquée 97

rappels des lois fondamentales

étude d'un plasma

influence du champ magnétique terrestre

Google

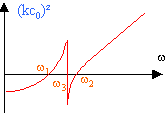
Il existe dans la haute atmosphère une couche ionisée contenant N=6 1011 électrons par m3, analogue au plasma précédent. La relation de dispersion du milieu s'écrit (kc0)² = w²-w0² avec w0²= Ne²/ ( me0). Il y a réflexion totale si la pulsation de l'onde est un peu inférieure à la pulsation de coupure w0 . On reçoit alors un écho important dû à cette couche. L'existence du champ magnétique terrestre complique ce phénomène d'écho.

Données : e = 1,6 10-19 C ; masse de l'électron me = 9 10-31 kg ; masse du proton mp = 1,67 10-27 kg ;

c0= 3 108 m/s ; m0 = 4p 10-7 H/m ; rayon de la terre R= 6370 km ; champ magnétique terrestre au sol : B0 = 4,7 10-5 T

les vecteurs sont écrits en gras et en bleu

  1. Soit un champ magnétique uniforme permanent B0.
  2. Etudier le mouvement d'une particule chargée, de masse m et de charge q, de vitesse initiale perpendiculaire au champ magnétique :
    - Montrer que la norme de la vitesse est constante et que le mouvement est plan.
    - Déterminer le vecteur rotation wc de la particule et le rayon de sa trajectoire.
    - La quantité wc est appelée pulsation -cyclotron : pourquoi ?
    - Quel mouvement a cette particule si la vitesse n'est plus perpendiculaire au champ ? Donner un exemple ( aucun calcul n'est demandé).
  3. L'onde plane étudiée précédemment se propage dans le plasma où règne ce champ magnétique uniforme permanent.
    - Expliquer pourquoi la théorie faite en II (" étude d'un plasma") reste valable si B0 est parallèle au champ électrique de l'onde et doit être modifiée s'il est perpendiculaire.
  4. Dans le cas où la théorie est modifiée, il faut remplacer la relation de dispersion ci-dessus (kc0)² = w²-w0² par :

    L'allure de la courbe (kc0)² est la suivante :

    - Déterminer à partir de la relation de dispersion les pulsations w1 et w2 telles que k =0 ainsi que w3 pour laquelle k tend vers l'infini en fonction de w0 et wc.
    - préciser les conditions sur w pour qu'il y ait propagation.

  5. On admetra qu'il y a réflexion totale pour k=0. Un émetteur situé à l'équateur, émet verticalement une onde plane sinusoïdale progressive dont on peut augmenter progressivement la longueur d'onde.
    - Si le champ électrique de l'onde est parallèle au champ magnétique terestre, on constate un écho lorsque la longueur d'onde atteint l0 = 42,7 m.
    -Si le champ électrique de l'onde est perpendiculaire au champ magnétique terestre, on constate un écho lorsque la longueur d'onde atteint l2 = 38,9 m.
    Retrouver pour la couche ionisée responsable de ces échos, le nombre d'électrons N par mètre cube et déterminer la valeur du champ magnétique qui y règne.
  6. Sachant que le champ magnétique terrestre peut être représenté comme celui dû à un dipole magnétique placé au centre de la terre dont les variations en fonction de l'altitude h sont telles que :

    Calculer l'altitude de la couche responsable de ces échos.

corrigé
particule chargée :

Le système étudié est la particule chargée. Le référentiel d'étude est supposé galiléen.

Le poids étant négligeable, la seule force appliquée est la force magnétique

La puissance de la force magnétique, force perpendiculaire à la vitesse, est nulle : en conséquence l'énergie cinétique de la particule est constante et la norme de la vitesse est constante (mouvement uniforme)

Appliquer le principe fondamental de la dynamique et projeter sur un axe parallèle au champ :

Compte tenu des conditions initiales y = 0 : Le mouvement reste dans le plan perpendiculaire au champ et contenant le vecteur vitesse initial.

Projection dans la base de Frenet :

mv²/R = |q| v B d'où le rayon R = mv / (|q|B)

tous les fateurs sont constants, en conséquence le rayon de courbure est constant : la trajectoire est un cercle de rayon R

v = Rwc d'où wc= |q|B/ m.

le vecteur rotation s'écrit :

wc : pulsation du champ électrique accélérateur dans le cyclotron synchronisé avec la vitesse de rotation des particules.

Cas où la vitesse n'est pas perpendiculaire au champ, il existe simultanément :

- un mouvement rectiligne uniforme suivant le champ magnétique

- un mouvement circulaire uniforme.

Les particules sont alors animées d'un mouvement hélicoïdal uniforme.

Les particules chargées s'enroulent autour des lignes de champ magnétique :

applications :

- focalisation à l'aide de lentilles magnétique (microscope électronique)

- réalisation de pièges magnétiques (le champ magnétique terrestre piège les particules chargées dans les ceintures de Van Allen)

dispersion :

Le champ électrique met les particules en mouvement. Si le champ magnétique est parallèle au champ électrique, il est parallèle à la vitesse des particules et en conséquence la force magnétique est nulle.

Il faut prendre en compte ces deux champs s'ils sont perpendiculaires.

k=0, le numérateur s'annule :

(w²-w0²)² -wc²w² = 0

(w²-w0²-wcw)(w²-w0²+wcw)=0

résoudre ces deux équations du second degré : seules les solutions positives ont une signification physique :

w²-wcw -w0² =0

D =wc² + 4w0²

k tend vers l'infini, le dénominateur s'annule :

w²-wc² -w0² =0 si w² = wc²+ w0²

il y a propagation si k² est positif soit :

w1 < w < w3 et w > w2.

calcul de N :

Les deux champs sont parallèles :

N = 9,1 10-31 * 8,82 10-12*4*3,14²*9 1016 / (42,7²*1,6² 10-38) =6,1 1011 électrons.

calcul du champ magnétique :

les deux champs sont perpendiculaires

w2= 6,28*3 108 / 38,9 = 4,843 107 rad/s.

k=0 donc (w2²-w0²)² -wc²w2² = 0

wc= (w2²-w0² ) / w2 avec w0= 6,28 * 3 108 / 42,7 = 4,412 107 rad/s.

wc= [ (4,843 107)²-(4,412 107)² ] / 4,843 107 = 8,23 106 rad/s.

le champ magnétique est calculé à partir de la relation : wc= |q|B/m

B= 8,23 106 *9,110-31 /1,6 10-19 = 4,68 10-5 T.

calcul de l'altitude :

(4,68 10-5/ 4,7 10-5 )exposant (-2/3 ) =1,002847

h² = R² * 2,847 10-3 = (6,37 106)²*2,847 10-3 =1,155 1011.

h = 340 km.

retour - menu