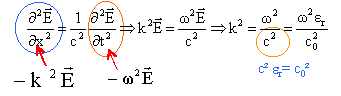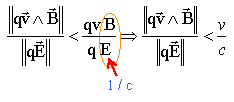|
rappels des lois fondamentales |
||
|
||
|
Le problème a pour objet l'étude de la propagation des ondes hertziennes dans la haute atmosphère. L'action du champ de pesanteur sera partout négligé. Données : e = 1,6 10-19 C ; masse de l'électron me = 9 10-31 kg ; masse du proton mp = 1,67 10-27 kg ; c0= 3 108 m/s ; m0 = 4p 10-7 H/m ; rayon de la terre R= 6370 km ; champ magnétique terrestre au sol : B0 = 4,7 10-5 T Etude d'un plasma : les vecteurs sont écrits en gras et en bleu; les lettres soulignés correspondent à des nombres complexes. On considère un plasma, milieu ionisé où se trouve des électrons libres, des ions positifs et des molécules neutres ; du point de vue macroscopique, ce milieu est toujours localement neutre. Ce plasma est un milieu suffisamment raréfié pour que, en première approximation, les interactions entre les particules n'interviennent pas.
corrigé |
||
|
Si la vitesse de phase vF = c/ n(w) dépend de la fréquence, alors il y a dispersion. En optique les rayons bleus sont plus déviés que les rayons rouges à travers un prisme: cela est dû à la dispersion. k est le vecteur d'onde. dériver deux fois E par rapport au temps et par rapport à x.
force de Lorentz :
Dans le cas d'une onde plane progressive B= E / c D'autre part la valeur maximum du produit vectoriel est vB : en conséquence
l'action de la force magnétique est négligeable devant l'action de la force électrique.
amplitudes : Système étudié : la particule chargée M ; le référentiel d'étude est supposé galiléen. Le poids et la force magnétique étant négligeables devant la force électrique, la seconde loi de Newton s'écrit :
On utilise la représentation complexe et on considère comme négligeable la variation de la phase de l'onde kx(t) L'amplitude des oscillations forcées est : s0 = |q|E0 / (w²m) le rapport des amplitudes du mouvement d'un électron et de celui d'un proton est égal à l'inverse du rapport de leur masse soit mP / me très supérieur à 1. l'amplitude du mouvement des protons est très faible par rapport à l'amplitude du mouvement d'un électron. Les protons sont considérés comme étant fixes. vecteur polarisation : Le vecteur polarisation s'écrit en considérant les protons fixes : P = - Ne se. Utiliser la notation complexe : d'une part se = eE / (mew²) et : P = -Nese = -Ne²E / (mew²) d'autre part P =e0(er-1)E e0(er-1) = -Ne² / (mew²) er-1 =-Ne² / (mew² e0 ) er =1-Ne² / (mew² e0 ). pulsation limite w0 : remplacer dans k² = w²er / c0² , er par l'expression ci dessus : k² = w²/ c0² [1-Ne² / (mew² e0 )] valeur de w correspondant à k=0 : 1=Ne² / (mew0² e0 ) mew0² e0 = Ne² w0² = Ne² / (me e0 ). aplication numérique : e0 m0 c0² =1 donne e0 =1 / (9 1016*4*3,14 10-7) = 8,84 10-12. w0² = 6,1 1011 *(1,6 10-19)² / (9,1 10-31* 8,84 10-12) = 1,94 1015. w0 = 4,4 107 rad/s. longueur d'onde associée l0 =2p c0/w0. l0 = 6,28 *3 108 / 4,4 107 = 42,8 m.
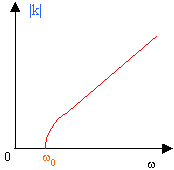
courbe k(w) :
Si w< w0, pas de propagation dans le milieu : il y a réflexion totale. l = 1376 m supérieur à l0 donc w< w0 et il y a réflexion sur la couche ionisée. Cette station aura une plus large audience. l = 2,85 m inférieur à l0 donc w> w0 et il y a propagation à travers la couche ionisée.
retour - menu |