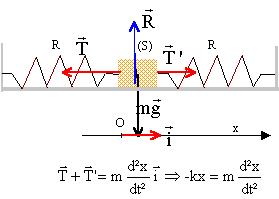
A oscillateur mécanique :

Une table à digitaliser est un dispositif permettant d'enregistrer les positions d'un système mécanique en fonction du temps.

Un solide S de masse m=100g, relié à une soufflerie réglable est accroché à deux ressorts identiques à spires non jointives. On enregistre la position de son centre de gravité G au cours du temps à l'aide d'un ordinateur connecté à la table à digitaliser horizontale.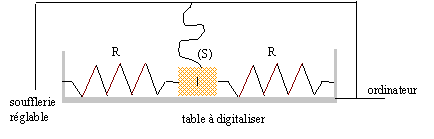

L'oscillateur décrit ci-dessus est équivalent à un solide de masse m accroché à un ressort unique de raideur k. La position du centre d'inertie G est repérée par son abscisse x .A l'équilibre le centre d'inertie G coïncide avec l'origine O du repère. On réalise trois enregistrements dans les conditions suivantes :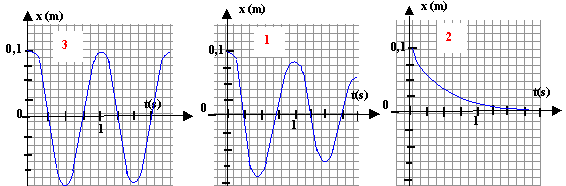
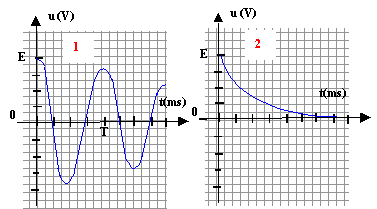
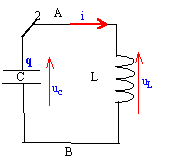
- a : soufferie à puissance maximale.
- b : puissance de la soufflerie légérement diminuée.
- c : puissance de la soufflerie fortement diminuée.

1. Indiquer pour chacun des trois enregistrements: la condition a, b, c de fonctionnement de la soufflerie, le régime d'évolution ( périodique, pseudo-périodique, apériodique)
2. Représenter au centre de gravité G les forces s'exerçant sur le solide S à l'instant t et les nommer.
   - En appliquant la deuxième loi de Newton, montrer que l'équation différentielle du centre d'inertie G du solide est : m d²x/dt² + kx = 0.
   - La solution analytique de l'équation différentielle est de la forme : x= X_M cos (2pt/T₀+F₀). Comment nomme-t-on les constantes X_M et F₀ ? Déterminer leurs valeurs sachant qu'à t=0 le solide S est laché sans vitesse au point d'abscisse x=10 cm.
   - Déterminer la période propre T₀ de l'oscillateur à partir de l'un des enregistrements précédents.
   - A l'aide d'une analyse dimensionnelle, déterminer l'expression de T₀ parmi les expressions suivantes :
   T₀ = 2p (m/k)^½; T₀ = 2p (k/m)^½; T₀ = 2p (m/k).
   - En déduire la valeur numérique de la constante de raideur k du ressort équivalent.
3. On étudie les différentes formes d'énergie du solide dans le cas du régime périodique.
   - Exprimer pour le système {ressort-solide} en fonction de m, k, x, v l'énergie cinétique Ec et l'énergie potentielle élastique Ep.
   - Donner l'expression de l'énergie mécanique E en fonction de Ep et Ec.
   - Que peut-on dire de l'énergie mécanique au cours du mouvement ?
   - Déterminer la valeur de l'énergie mécanique à t=0 et en déduire la vitesse de passage du solide à la position d'équilibre.
   - Le schéma ci-dessous représente les différentes formes d'énergie au cours du temps. Identifier chaque courbe. Justifier.

   - Dans le cas d'un régime pseudo-périodique pourquoi l'énergie mécanique diminue-t-elle au cours du temps ?

B Application des oscillations électriques :

Pour mesurer le taux d'humidité relative de l'air ( % d'HR) on peut utiliser le capteur appelé "humidistance" dont le principe utilise un condensateur de capacité variable avec l'humidité. On place ce condensateur dans le circuit ci-dessous dans lequel la bobine a une résistance négligeable.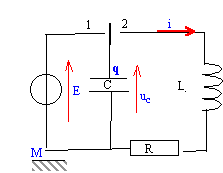

L'interrupteur est d'abord placé en position 1 pour charger le condensateur, puis basculer en position 2 pour le décharger. Un système informatisé d'acquisition de données permet de relever la tension aux bornes du condensateur au cours de la décharge.

1. Suivant la valeur de la résistance R non nulle, l'évolution du système (RLC) se fait suivant deux régimes différents. Tracer l'allure de la tension aux bornes du condensateur en fonction du temps pour ces deux régimes que l'on nommera.
2. On suppose maintenant que R=0 . Reproduire la partie du circuit correspondant à la décharge . Etablir l'équation différentielle régissant l'évolution de la charge q du condensateur.
3. Vérifier que l'expression q= Q_M cos (2pt/T₀+F₀) est solution de l'équation différentielle si la période propre T₀ a pour expression : T₀ = 2p (LC)^½.
4. Le condensateur du capteur d'humidité est introduit dans le circuit précédent. La période mesurée T vaut 31,4 ms dans les conditions atmosphériques de l'expérience. Sachant que l'inductance de la bobine L=200 mH, calculer la capacité du condensateur.
5. On lit sur la notice de l'appareil :
   gamme de mesures 10 à 100 % d'HR ; sensibilité 0,4 pF par % d'HR ; capacité à 25°C et à 43% d'HR : 122 pF ; température d'utilisation : 0 à 85 °C.
   - L'expression de la capacité C du condensateur est une fonction affine croissante du taux d'HR noté h, exprimé en % d'HR. On peut donc écrire C=a h + b. Déterminer les valeurs des constantes positives a et b.
   - Dans le cadre des données ci-dessus déterminer le %d'HR de l'atmosphère.

    

---

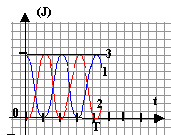
corrigé

---

enregistrement 3 : régime périodique ; puissance maximale

enregistrement 1 : régime pseudo-périodique ; puissance un peu diminuée

enregistrement 2 : régime apériodique ; puissance fortement diminuée

X_M : amplitude des oscillations (m) et F₀ phase à t= 0, instant initial.

X_M = 0,1 m ; F₀ = 0, car à t=0 l'abscisse x est égale à 0,1 m.

d'après l'enregistrement 3 la période T₀ vaut 1s.

masse m : kg ; raideur k : force (N) longueur^-1 avec : force= masse accélération soit kg m s^-2.

k : kg m s^-2 m^-1 ou kg s^-2 ;

m / k : kg kg^-1 s² = s² ; (m/k)^½ s'exprime en seconde et 2p est sans dimension

en conclusion T₀ = 2p (m/k)^½;

T²₀ =4p² mk^-1 soit k = 4p² m/T²₀ = 4*3,14² *0,1/ 1 = 3,95 Nm^-1.

L'énergie mécanique (courbe 3) est la somme de l'énergie potentielle et de l'énergie cinétique

à t = 0 l'énergie mécanique est sous forme potentielle élastique Ep=½kX²_M. La courbe (1) représente Ep

au passage à la position d'équilibre ( t= 0,25 T₀) l'énergie mécanique est sous forme cinétique Ec = ½mv². La courbe (2) représente Ec

E(t=0 )= ½kX²_M = 0,5 *3,95*0,1² = 0,02 J.

vitesse du solide au passage à la position d'équilibre : 0,02 = 0,5*0,1 v²

v² = 0,4 ; v = 0,63 m/s.

Dans le cas d'un régime speudo-périodique une partie de l'énergie mécanique est perdue dans les frottements mécaniques.

---

(1) régime pseudo-périodique: R faible

(2) régime apériodique : R élevée.

u_c=u_L soit q/C = Ldi/dt avec i = -dq/dt ( décharge) et di/dt = -d²q/dt² = -Lq"

q/C = -Lq" soit q"+ w₀² q=0 avec w₀² =(LC)^-1 et 2p/T₀= w₀.

q= Q_M cos (w₀+F₀) ; dérivée première par rapport au temps q' = Q_M w₀( -sin(w₀+F₀))

q" = -Q_M w²₀cos (w₀+F₀) = - w²₀q

repport dans l'équation différentielle de la charge : - w²₀q + w²₀q= 0 , vérifiée quel que soit t.

capacité :

T =2p (LC)^½ soit T²= 4p² (LC) d'où : C= T²/ (4p²L)= (31,4 10^-6)²/( 4*3,14²*0,2) = 1,25 10^-10 F= 125 pF.

a= 0,4 pF %HR^-1.

122 = 0,4 * 43+b d'où b = 104,8 pF

C= 0,4 h +104,8.

h=(C-104,8 )/ 0,4 = (125-104,8) / 0,4 = 50,5 % d'HR.

---