dipole RLC oscillations forcées cours exercices dipole LC : oscillations libres
Le générateur impose sa propre fréquence. lorsque la fréquence du générateur est ègale à la fréquence propre du dipole : il y a résonance d'intensité la résonance est aigue si la résistance du circuit est faiblle; elle est d'autant plus floue que R est élevée	bande passante: ensemble des fréquences telles que l'intensité soit supérieure à la valeur maxi divisée par 1,414
intensité et tension aux borne du dipole sont alors en phase
l'intensité passe par un maximum et l'impédance Z passe par un minimum égal à la résistance du circuit
on observe une surtension aux bornes du condensateur égale au facteur de qualité fois la tension aux bornes du dipole
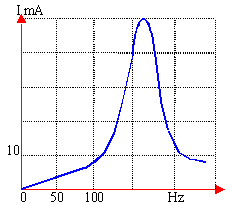
exercice 1 oscillations forcées - circuit RLC La valeur éfficace de la tension aux bornes du circuit est constante, égale à 2 V. On fait varier la fréquence du GBF. On obtient la courbe de résonance ci contre. inductance de la bobine L=1 H . vrai ou faux La valeur de la résistance du circuit est R=20 W La capacité du condensateur est d'environ 1 mF la bande passante est voisine de 30 Hz Pour diminuer la bande passante du circuit il suffit de diminuer la résistance du circuit. corrigé faux A la résonance , l'impédance du circuit est minimale,égale à la résistance totale du dipole RLC. Il faut diviser la tension aux bornes du circuit par l'intensité maxi male du courant en ampère 2/0,04 =50W vrai à la résonance la fréquence du GBF est égale à la fréquence propre du dipole RLC c'est à dire f0 voisin de 160 Hz d'où C=1 divisé par ((160*2*3,14)2*1)=10-6 F vrai la bande passante est l'ensemble des fréquences telles que l'intensité soit supérieue à l'intensité maximale (valeur de I à la résonance ) divisée par 1,414. lire sur le graphe pour I=40/1,414 =28,3 mA vrai la largeur de la bande passante est proportionnelle à la résistance du circuit. Un résonance dite aigue est obtenue si R diminue exercice 2 résonance- circuit RLC- puissance Un dipole RLC (C=10-9 F ; L=1 H ) est alimenté par une tension u(t)=10cos(wt) Quelle est la fréquence propre du dipole ? Lorsque la fréquence du générateur est égale à la fréquence propre, la valeur maximale de l'intensité est 1 mA. Quelle est la résistance du circuit ? Le facteur de qualité est Q=4,45. En déduire la bande passante. Quelle est la puissance P0 fournie au dipole par le générateur à la fréquence propre. A une fréquence supérieure à la fréquence propre, comparer la puissance moyenne P fournie au circuit à P0. corrigé fréquence propre f0= 1/ T= 5035 Hz La fréquence du générateur est égale à la fréquence propre : phénomène de résonance d'intensité. L'intensité efficace passe par une valeur maxi et l'impédance du circuit par une valeur minimale , égale à la résistance . R=Umax / I max= 10/0,001 =104 ohms Q=f0 /Df ; Df = 5035/4,45 = 1131 Hz puissance consommée P=U eff Ieff cos(j) à la résonance tension et intensité sont en phase cos(j)=1 ; Uefficace=U maxi/1,414 ; Iefficace=Imaximale / 1,414 P=10/1,414*10-3/1,414= 5 milliwatts sinon l'intensité efficace est inférieure à 1 mA de plus tension et intensité sont décalées (déphasées) cos(j)<1 donc la puissance consommée est inférieure à 5 mW exercice 3 étude d'oscillogrammes Z est un dipole de nature inconnue. L'échelle est la même sur les deux voies de l'oscilloscope. L'ensemble est alimenté par une tension sinusoidale. Aux bornes d'une capacité pure la tension est en retard de p/2 sur l'intensité. Aux bornes d'une self pure la tension est en avance de p/2 sur l'intensité. quelle est la proposition correcte ? Z est une résistance. Z est une bobine inductive. Z est un condensateur. Peut-on calculer la valeur de Z si R=1000 W ? corrigé Sur la voie 2 on visualise la tension UBM aux bornes d'un résistor. 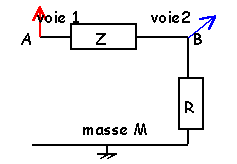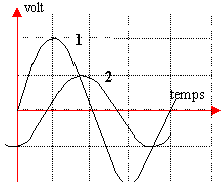C'est l'image de l'intensité UBM=1000 i Sur la voie 1 on visualise la tension UAM aux bornes du dipole Z et R en série. la courbe 1 est en avance sur la courbe 2 d'environ p/2 : Z est une bobine inductive lorsque deux fonctions sinusoidales varient dans le même sens, la première qui passe par un maximum est en avance sur l'autre. Les lois du courant continu ne s'appliquent pas en général en courant alternatif. Z et R sont en série , mais : UAM maxi est différent de (Z+R)Imaxi UAM maxi est différent de UAB maxi +UBM maxi UAM maxi cos(wt+j)= UAB maxi cos(wt+p/2) +UBM maxi cos(wt) On ne peut pas calculer Z exercice 4 circuit RLC courbes intensité tension- régime forcé On associe en série un GBF, délivrant une tension sinusoidale d'amplitude 5V, un résistor R, un condensateur de capacité C, et une bobine inductive d'inductance L .R=100W; C=8mF; L=0,3H. Un oscilloscope visualise la tension aux bornes du dipole (voie A) ainsi que l'intensité (voie B) 2ms / div ; 2V / div. Les branchements de l'oscilloscope sont: masse en D; voie A en A; voie B en E. la courbe 1 représente la tension aux bornes du dipole RLC. l'intensité éfficace Ieff vaut 40 mA. L'impédance Z vaut 125 ohms. corrigé faux pour visualiser la tension UAE, aux bornes du dipole RLC, il faut relier E à la masse et A à la voie A. Visualiser l'intensité, c'est visualiser la tension aux bornes d'un résistor UDE=Ri. 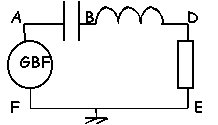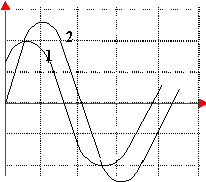Il y a une seule mase dans un circuit; voie B en D faux La courbe 2 (amplitude 5V) représente la tension aux bornes du dipole RLC faux tension aux bornes du résistor=100 fois intensité tension maxiUDE:4V lecture courbe 1 4=100*Imaxi Imaxi=rac carrée (2) *Iefficace Ieff=40/1,414=28,2 mA vrai tension maxi aux bornes dipole= impédance Z fois intensité maxi Z=5/0,04=125 ohms exercice 5 étude courbe de résonance- fréquence propre 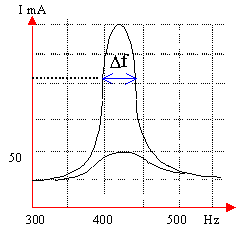Soit un circuit RLC en régime forcé C=1mF; bobine d'inductance L, résistance r; la valeur de la résistance R peut varier. La tension éfficace délivrée par le GBF est constante 4,5 V. En faisant varier la fréquence du GBF on observe les courbes ci contre. vrai ou faux La courbe 1(pic aigu) correspond à R=100W et l'autre courbe à R=20W. La fréquence propre du dipole est voisine de 425 Hz et le facteur de qualité est proche de 14 (courbe1). L'inductance de la bobine est L=0,14H. La résistance de la bobine vaut 30 ohms. corrigé faux La résonance est d'autant plus aigue (pic étroit) que la résistance du circuit est faible. La courbe 1 correspond à la plus petite valeur de R. vrai L'intensité efficace passe par un maximum (phénomène de résonance)lorsque la fréquence du GBF est égale à la fréquence propre du dipole RLC. lecture graphique f=425 Hz et I0=150 mA La bande passante est un intervalle de fréquence telle quel'intensité maxi soit supérieure à I0 divisée par radical de 2 soit 150/1,414,=106mA lecture graphique 410<f<440 soit Df=30Hz Le facteur de qualité est la fréquence propre divisée par la bande passante 425/30=14 vrai 1/425=6,28 rac carée(LC) période propre du dipoleRLC LC=1 / (425*6,28)² d'où L=0,14H faux à la résonance l'impédance est égale à la résistance totale du dipole RLC. Z=Ueff /Ieff =4,5/0,15 =30 ohms R+r=30 avec R=20 ohms donc la résistance de la bobine est 10 ohms. retour - menu