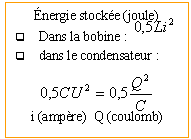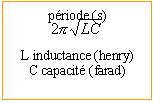dipole LC oscillations libres cours exercices
RLC : oscillations forcées
il y a un échange permanent d'énergie entre la bobine et le condensateur. le dipole est le siège d'oscillations libres d'autant plus amorties que la résistance est grande	énergie
période
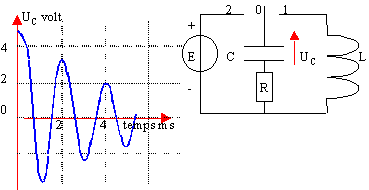
exercice 1 oscillations électriques - circuit (RLC) Soit un circuit RLC alimenté par un générateur de signal rectangulaire. L=4,9 mH et C=10-8F On visualise sur l'écran d'un oscilloscope la tension aux bornes du condensateur, et on constate que l'amplitude des oscillations est quasi nulle après dix oscillations. La période propre des oscillations est d'environ 0,22 ms vrai ou faux La fréquence du signal rectangulaire du générateur basse fréquence doit être supérieure à 2200Hz pour que l'on puisse observer le phénomène. L'écran de l'oscilloscope, ayant une longueur de 10 cm, ce qui représente 10 divisions, la vitesse du balayage choisie est de 5ms/division pour n'observer qu'un seule oscillation . Pour observer un plus grand nombre de'oscillations, on augmente la valeur de la résistance R. corrigé faux 6,28*racine carrée(4,9 10-3 * 10-8)=4,4 10-5 s faux dix périodes propres de l'oscillateur=4,4 10-4 s ; la demi période du signal carré du générateur doit être supérieure ou égale à cette valeur. Période du générateur >8,8 10-4 s fréquence du générateur inférieure à 10000/8,8 soit inférieure à 1136 Hz faux 10 divisions correspondent à 50 ms valeur bien supérieure à la période propre de l'oscillateur. Il faudrait choisir 5 microsecondes par division pour observer sur tout l'écran une seule période faux En augmentant la résistance on augmente l'amortissement ; on observera moins de 10 oscillations. 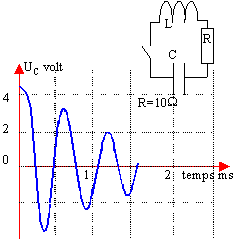exercice 2 oscillations libres amorties - dipole(RLC) Le condensateur est préalablement chargé . A la date t=0 on ferme l'interrupteur. On enregistre la tension aux bornes du condensateur en fonction du temps. L=1 H ; R=10 W la pseudo période est de l'ordre de 0,62 ms La capacité du condensateur est voisine de 10nF L'énergie initialement stockée dans le condensateur etait proche de 125 mJ A la date t=0,75 période la bobine stocke toute l'énergie. corrigé vrai 4 pseudo périodes valent environ 2,5 ms donc la pseudo période est proche de 0,62 ms vrai la fréquence propre du dipole RLC est (voir ci contre) avec f0=1/ 6;2 10-4 Hz =16000Hz et L=1 Hd'où C=10 nF   faux L'énergie initialement stockée dans le condensateur est : tension initiale 5V (lecture sur le graphe) 0,5 *10-8* 52=12,5 10-8 J=1250 mJ vrai à t=0,75 période la tension aux bornes du condensateur est nulle ( voir graphe) la bobine stocke toute l'énergie il y a un échange permanent d'énergie entre condensateur et bobine. Au cours de ces échanges une partie de l'énergie est perdue par effet joule dans le résistor. 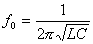E=0,5 C U2 exercice 3 décharge oscillante- circuit RLC libre Le condensateur est initialement déchargé. E=5V ;R=20 W ;C=1 mF (répondre vrai ou faux) On bascule l'interrupteur en position 2 ;1 ms plus tard, l'énergie stockée par le condensateur est 12,5 microjoules. A la date t=0, on bascule l'interrupteur en position 1 et on enregistre la variation de uC en fonction du temps. On en déduit que L=0,1H. L'amortissement dépend de la valeur de la résistance R. On recommence une série de manipulations avec E=10 V au lieu de 5V. On observe des oscillations électriques de fréquence double soit 1000 Hz. corrigé vrai constante de temps 20*10-6=2 10-5 s au dela d'une durée supérieure à 5 fois la constante de temps la charge est terminée et la tension au borne du condensateur est E. Energie stockée par le condensateur : 0,5*10-6*5²=12,5 mJ vrai période (lecture graphique)= 2 10-3 s LC=4 10-6 /6,28² vrai la diminution de l'amplitude dépend de la résistance totale du circuit faux l'amplitude initiale de la tension est 10 V par contre la fréquence et la période sont indépendante de E; la fréquence est l'inverse de la période soit 1/2 10-3 =500 Hz constante de temps du dipole RC t=RC en seconde Energie stockée par le condensateur    0,5 CU²     période du dipole LC 6,28 rac.carrée(LC) exercice 4 transfert d'énergie entre bobine et condensateur Un condensateur de capacité C=20 nF est initialement chargé sous une tension E=10 V. Il se décharge ensuite à travers une bobine d'inductance L=0,05 H et de résistance r. L'énergie dissipée par effet Joule dans la résistance au cours de la décharge (débutant à l'instant t=0) est égale au sixième de l'énergie initiale stockée dans le condensateur. Montrer que l'intensité maximale du courant est atteinte lorsque le condensateur est déchargé. Calculer la valeur Im de cette intensité. A quel instant a t'on i=Im . 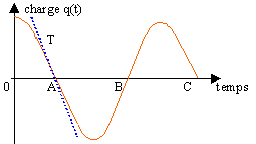corrigé Sur la courbe ci dessus, la valeur absolue du coefficient directeur de la tangente T à la courbe passe par une valeur maximale en A quand la charge du condensateur est nulle. 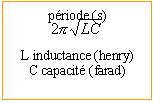Or ce coefficient directeur représente l'intensité i = dq/dt = q' Energie initiale stockée par le condensateur : 0,5 CE² en fin de décharge (point A), l'énergie stockée par la bobine est égale à : 5/6 *0,5 CE² = 0,5 L Im² Im² = 5 CE²/ (6L) Im² = 5*20 10-9 *10² /(6*0,05)= 3,33 10-5 d'où Im=5,8 mA Le point A correspond au quart d'une pseudo-période tA= 3,14/2 racine carrée (0,05*20 10-9) tA= 49,6 microsecondes
exercice 5 On étudie deux circuits réalisés avec une même bobine de résistance négligeable et d'inductance L mais le premier circuit utilise un condensateur de capacité c=0,1µF et le second un condensateur de capacité C'. Dans les deux cas,le condensateur utilisé est chargé puis ses bornes sont déconnectées et reliées à celle de la bobine. La tension entre les armatures des condensateurs est visualisée sur un oscilloscope. L'oscilloscope a été obtenu avec une base de temps fixée à 0,2ms/division et une amplification verticale de 2V/div. Le circuit 1 (C=0,1µF) a une période de 0,8ms et le 2 une période de 0,4ms. L' amplitude des tensions pour les deux circuits est de 6V. Déterminer la valeur de L. Déterminer la valeur de C'. Calculer l'énergie dans chacun des deux circuits oscillants. En déduire l'intensité maximale de courant dans chacun des deux circuits. corrigé circuit n°1 : LCw² = 1 w = 6,28 / période en seconde = 6,28 / 0,8 10-3 = 7850 rad/s C = 10-7 F ; L = 1 / (7850² *10-7 ) = 0,162 H. circuit n°2 : w = 6,28 / 0,4 10-3 = 15 700 rad/s LC' w ²=1 C' = 1 /(0,162 * 15 700² ) =2,5 10-8 F. énergie : lorsque le condensateur stocke toute l'énergie : E =½ C U² max . échange permanent d'énergie entre bobine et condensateur. lorsque la bobine stocke toute l'énergie E= ½L i² max . circuit n°1 : 0,5*10-7 *6² = 1,8 mJ. i max = rac carrée ( 2*1,8 10-6 / 0,162) = 4,7 mA. circuit n°2 : 0,5 *2,5 10-8 *6² = 0,45 mJ. i max = rac carrée ( 2*0,45 10-6 / 0,162) = 2,35 mA.
retour - menu