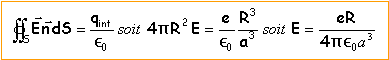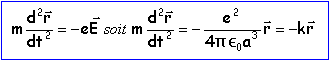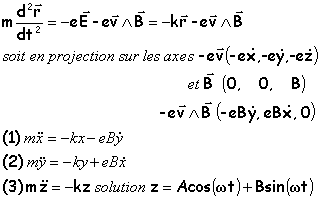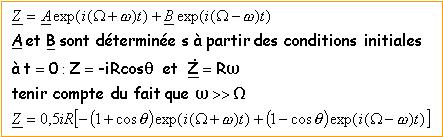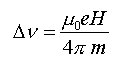millikan

	le modèle d'atome de Thomson (1897) Les atomes, selon Thomson, sont constitués : d'une sphère pleine chargée positivement de manière uniforme. le rayon de la sphère est de l'ordre de 10^-10 m d'électrons qui peuvent vibrer librement à l'intérieur de la sphère. l'atome reste électriquement neutre. Ce modèle n'était pas capable d'expliquer les raies du spectre d'émission de l'hydrogène. Il ne précisait pas la nature de la matière constituant la sphère positive, ni la densité de charge.
1 modèle de Thomson de l'atome d'hydrogène	L'électron de l'atome d'hydrogène se déplace dans le champ électrostatique du proton représenté par une distribution volumique de charges uniforme de rayon a. L'électron reste toujours a une distance R du proton inférieure à a. Données : a=5 10^-11 m ; masse de l'électron 9,1 10^-31 kg charge de l'électron -1,6 10^-19 C. En l'absence de champ extérieur, montrer que le mouvement de l'électron est celui d'un oscillateur harmonique de constante de rappel k= e²/(4pe₀a³)
	corrigé L'électron n'est soumis qu'au champ électrique crée par une distribution volumique censée représenter le proton. Ce champ est radial. Appliquons le théorème de Gauss à une sphère de centre O (centre de l'atome), de rayon R < a. Dans un référentiel supposé galiléen, lié au proton, le pricipe fondamental appliqué au proton s'écrit : L'électron est donc soumis à une force de rappel proportionnelle au déplacement représenté par le vecteur r. L'électron éffectue des oscillations sinusoïdales autour de sa position d'équilibre (située en O, centre de l'atome), de pulsation w²=k/m.
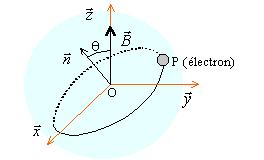
2 l'atome d'hydrogène est placé dans un champ magnétique uniforme	L'atome d'hydrogène est placé à la date t=0 dans un champ magnétique uniforme. Avant l'application de ce champ, l'électron est supposé se déplacer sur une orbite circulaire de rayon R< a dont la normale forme un angle q avec Oz. Déterminer la fonction z(t) pour t positif. Les conditions initiales sont z= Rsinq et z'= 0.
	corrigé en tenant compte des conditions initiales z= Rsinq cos(wt)
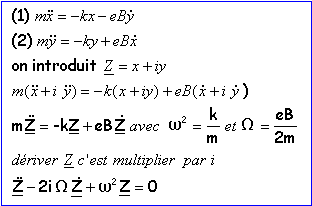
3 résolution d'équation différentielle utilisant les nombres complexes	si B= 1 T; alors w=4,5 10¹⁶rad s^-1; W=8,8 10¹⁰ rad s^-1.
	En déduire les fonctions x(t) et y(t). Montrer que le mouvement de l'électron est la superposition d'un mouvement sinusoïdal de pulsation w le long de l'axe Oz, d'un mouvement circulaire direct de pulsation w+W et d'un mouvement circulaire indirect dans le même plan, de pulsation w-W. corrigé équation caractéristique de l'équation différencielle ci dessus : r²-2iWr+w²= 0 D=-4(W²-w²)= voisin de (2 i w)² racines de cette équation voisines de : i(w+W ) et i(-w+W ) La fonction x(t) correspond à la partie réelle de ce nombre complexe. La fonction y(t) correspond à la partie imaginaire de ce même nombre. x(t)=0,5R[(1+cosq)sin(w+W)t +(1-cosq)sin(w-W)t ] y(t)=0,5R[-(1+cosq)cos(w+W)t +(1-cosq)cos(w-W)t ] Le mouvement de l'électron peut être assimilé aux mouvements de 3 particules fictives. Le mouvement de P₁ est circulaire de pulsation w+W dans le sens trigonomètrique direct. Celui de P₂ est circulaire, de pulsation w-W dans le sens trigonométrique inverse. A cela s'ajoute le mouvement oscillatoire le long de l'axe Oz.
4 effet Zeeman	On appelle effet Zeeman, la décomposition des niveaux énergétiques et des raies spectrales d'une substance rayonnante sous l'action d'un champ magnétique extérieur.
	effet Zeeman longitudinal observé dans la direction du champ : chaque raie spectrale se dédouble en deux composantes de fréquence n+Dn et n-Dn où n est la fréquence de la raie en l'absence de champ extérieur . effet Zeeman transversal observé dans le plan perpendiculaire au champ : Aux deux raies spectrales précédentes il faut ajouter une raie de fréquence n. L'intervalle Dn entre les raies coïncide avec la fréquence de Larmor e et m représentent la charge et la masse de l'électron, H le champ extérieur. La grandeur Dn est habituellement très petite Dn / n est de l'ordre de 10^-5 pour des champs supérieurs à 1 T. retour - menu