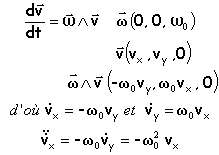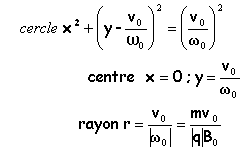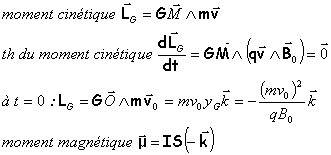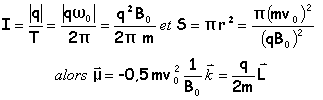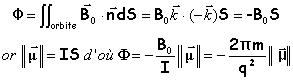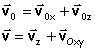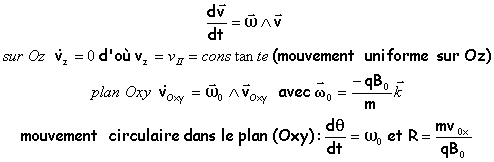La physique des plasmas

Qu'est ce qu' un plasma ? C'est un milieu constitué d'atomes ou de molécules en partie ionisé ou en totalité. L'ensemble reste électriquement neutre. La création d'un plasma nécessite un apport d'énergie important.

Les réactions de fusion nucléaires au coeur des étoiles sont un exemple de plasma chaud (température supérieure à 106 K).

Un plasma froid (T< 105 K) est obtenu en appliquant un champ électrique à un gaz injecté dans un enceinte sous des pressions comprises entre 1 mbar et 1 mbar. Les plasmas froids sont utilisés dans les traitements de surface, la gravure des circuits en microélectronique, les dépots de couches minces à des fins de protection ou de décoration.
1

particule chargée dans un champ magnétique uniforme
Données : masse de l'électron 9,1 10-31 kg charge de l'électron -1,6 10-19 C.

1 / (4 p e0)=9 109 SI; m0=4p 10-7 SI; masse du proton 1,67 10-27 kg

Les forces de pesanteur sont négligées et on se place dans le cas de la mécanique de Newton. Une particule de masse m, de charge q, animée d'une vitesse v0 pénètre dans une région où règne un champ magnétique uniforme. Les vecteurs vitesse et champ sont orthogonaux.

  1. Ecrire l'équation différentielle du mouvement sous la forme :

exprimer w0 et montrer que le mouvement est uniforme.

  1. Exprimer les coordonnées de la vitesse et de la position de la particule (à l'instant t=0, la particule est en O, origine du repère). Montrer que la trajectoire est un cercle dont on précisera le centre et le rayon r.
  2. Application numérique : B=5 mT calculer r et w0 dans les 2 cas suivants :
  • électron d'énergie cinétique 1 keV
  • proton d'énergie 100 keV
 

corrigé

Le référentiel du laboratoire étant supposé galiléen, la relation fondamentale de la dynamique s'écrit :

La force magnétique étant perpendiculaire au vecteur vitesse à chaque instant , elle ne modifie pas l'énergie cinétique : la norme de la vitesse est constante et le mouvement est uniforme.

Projections de l'équation différentielle ci dessus sur les axes:

vitesse tenant compte de la vitesse initiale (vx=v0 et vy=0)

vx=v0 cos(w0 t) et vy=v0 sin(w0 t)

position de la particule ( primitives de vxet vy et x0=y0=0)

x = v0 /w0sin(w0 t) et y = v0 /w0(1-cos(w0 t ))

trajectoire :

dans le plan (Oxy) car la vitesse initiale n'a pas de composante suivant Oz

application numérique :

électrons : w0=8,8 108 rad s-1 ; r=2,1 cm

protons : w0=-4,8 105 rad s-1 ; r=9,1 m

2

moment cinétique et moment magnétique
  1. Exprimer le moment cinétique par rapport à G , centre de la trajectoire en fonction de m, v0, q et B0.
  2. Indiquer sur un schéma les trajectoires des électrons et des protons, les moments magnétiques associés.
  3. Montrer que la norme du moment magnétique est proportionnelle au flux du champ magnétique à travers l'orbite de la particule.

corrigé 

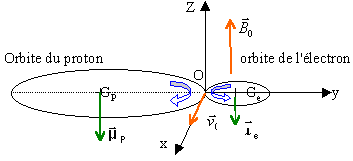
moment cinétique de la particule par rapport au centre de la trajectoire

relation entre moment cinétique et moment magnétique

flux du champ magnétique à travers l'orbite de la trajectoire 

le moment magnétique et le flux sont proportionnels

3

la vitesse initiale est quelconque
La vitesse initiale est orientée d'une manière quelconque par rapport au champ magnétique. Quelle est le mouvement de la particule ?

composantes initiales de la vitesse

composantes à la date t de la vitesse suivant Oz et dans le plan (Oxy)

 

Montrer que la projection de ce mouvement dans le plan (Oxy) est un cercle de rayon R et de vitesse angulaire dq / dt. Donner leurs expressions.

corrigé

La force magnétique perpendiculaire à la vitesse à chaque instant ne modifie pas l'énergie cinétique. La norme de la vitesse est constante.

L'équation différentielle du mouvement (question 1) donne en projection sur oz et dans le plan (Oxy)

retour - menu