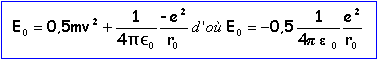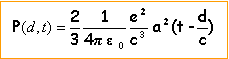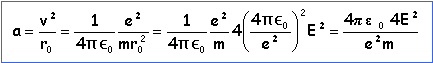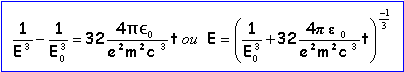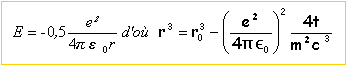perte d'énergie de l'atome d'hydrogène par rayonnement

L'atome d'hydrogène est représenté par un noyau immobile O de charge +e, autour duquel un électron (charge -e et masse m) décrit un mouvement circulaire uniforme.

e=1,6 10-19 C, m=9,1 10-31 kg ; c=3 108 ms-1.

1 /(4pe0)=9 109 SI. r0=0,53 10-10 m
1

accélération, vitesse, énergie de l'électron

 

  1. Exprimer l'accélération, la vitesse, l'énergie de l'électron.
  2. Faire les applications numériques.
  3. Quelle est la période de l'électron (durée pour décrire un tour)
 

corrigé

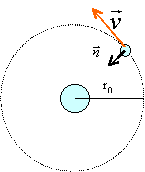
Le mouvement de l'électron étant circulaire uniforme, le vecteur accélération est centripète, dirigé vers O, de norme vitesse ² divisée par le rayon : v²/r0.

Dans un référentiel lié au noyau immobile, le principe fondamental de la dynamique s'écrit : (poids de l'électron négligeable devant les forces attractives de Coulomb)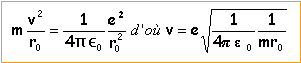

v= 2,19 106 m s-1.

aspect énergétique : somme de l'énergie cinétique et de l'énergie potentielle d'origine életrostatique. (origine à l'infini)

E0=-2,17 10-18 J ou -13,6 eV

durée nécessaire pour faire un tour, circonférence de rayon r0 :

t=2pr0 /v = 1,5 10 s

2

Une charge accélérée rayonne de l'énergie
Une charge accélérée rayonne de l'énergie. L'énergie rayonnée par l'électron est faible devant l'énergie totale de l'électron, en conséquence la trajectoire reste à peu près circulaire avec une diminution lente du rayon.

Puissance rayonnée dans le vide par un électron accéléré à une distance d très grande devant r0. (a est l'accélération)

L'électron émet une onde électromagnétique. L'onde arrivant à la distance d, est l'onde émise par la source à l'instant t-d/c.

  1. Quelle relation lie la puissance rayonnée et l'énergie perdue par l'électron ?
  2. Déterminer l'équation différentielle vérifiée par l'énergie ?
  3. Tenir compte des conditions initiales pour exprimer la loi d'évolution de l'énergie.
  4. Donner l'évolution du rayon de la trajectoire au cours du temps et conclure.

corrigé

Soit E l'énergie mécanique de l'électron à la date t , la puissance rayonnée (positive) vaut P=-dE /dt.

dE est l'énergie perdue par l'électron pendant la durée dt.

expression de l'accélération à partir des données des questions précédentes

d'où la puissance rayonnée :

intégrer en tenant compte des conditions initiales r(t=0)=r0 et E (t=0) =E0.

En tenant compte de l'expression de l'énergie (voir 1) on déduit la loi de r(t)

Le rayon diminue : ce modèle conduit à un atome instable. Seule la mécanique quantique sera capable de passer cette difficulté.

retour - menu