roulement ou glissement sur un plan incliné

Google

1

théorèmes de la mécanique du solide

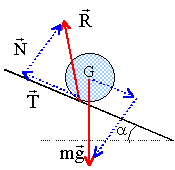
Une roue pleine et homogène de masse M, rayon R, centre G, roule sans glisser sur un plan incliné d'angle a. Nous prenons pour axe OX orienté vers le bas la droite formée par les projetés de G sur le plan incliné. La roue reste verticale. Soit X(t) l'abcisse de A et de G sur OX, avec X=0 à t=0. On se propose de > trouver l'accélération Ax de son centre de masse en appliquant à la roue les principes de la dynamique des solides.

  1. Ecrire le théorème de la quantité de mouvement et en déduire deux relations reliant les composants T et N de la réaction R du plan, au poids mg de la roue et à l'angle a.
  2. On a le droit d'écrire le théorème du moment cinétique par rapport au point G.
    a) En déduire une troisième relation reliant Tà l'accélération angulaire dw/dt.
    Retrouver la valeur de Ax en fonction de g et de a à partir du théorème de l'énergie cinétique.
    b) Donner la valeur de T et N en fonction de mg et a. A partir de quelle valeur de a la roue ne peut elle plus rouler sans glisser si le coefficient dynamique est 0,5?

     

corrigé

La roue est soumise à son poids, à l'action du plan décomposée en une action

normale au plan N et une action parallèle au plan T , de sens contraire à la vitesse.

somme vectorielle des forces = masse fois vecteur accélération de G

sur un axe perpendiculaire au plan l'accélération est nulle (pas de décollage)

N = mg cos a (1)

sur un axe parallèle au plan orienté vers le bas:

-T + mg sin a = m Ax (2)

le signe moins traduit une force de freinage

 

théorème du moment cinétique en G, centre d'inertie de la roue:

T* rayon= I dw/dt avec I = ½m r² roue cylindrique pleine.

T= ½ mr dw/dt avec Ax = r dw/dt soit T = ½ mAx (3)

les moments des autres forces , poids et N sont nuls car leur direction

rencontrent l'axe de rotation

repport ci-dessus en (2)

-½mAx + mg sin a = m Ax d'où Ax =2/3 g sin a et T = 1/3 mg sin a.

 

il n'y a pas de glissement tant que T inférieure ou égale à f N

1/3 mg sin a <= 0,5 mg cos a

tan a <= 1,5 soit a <= 56,3°.

retrouver l'accélération de G à partir du th de l'énergie cinétique :

au départ , pas d'énergie cinétique, la vitesse étant nulle

à une date t : Ec fin =½ mv² + ½ Iw².

avec I=½ mr² et w=v/r d'où : Ec fin = ½ mv² + ½ ( ½mr² v² / r²)= 0,75 mv²

variation d'énergie cinétique : 0,75 mv²

seul le poids travail tant qu'il n'y a pas glissement

W poids = mg AB sina.

par suite 0,75 mv² = mg AB sina.

v² = 2(2/3 g sin a ) AB

relation du type : v² = 2Ax AB alors Ax = 2/3 gsin a.

retour - menu