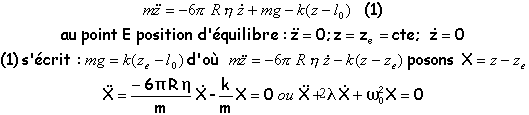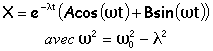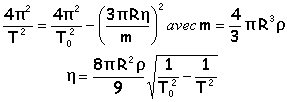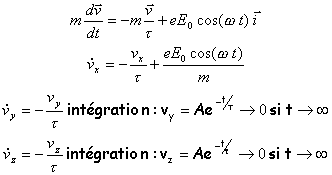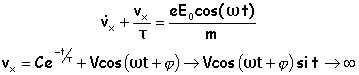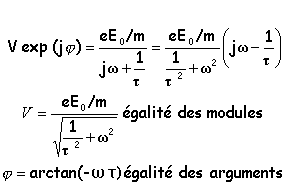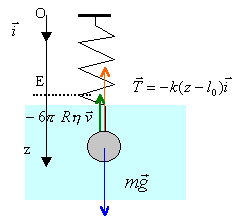
La raideur du ressort est k et sa période d'oscillation dans l'air est T₀.

Ecrire l'équation différentielle en X = (z-z_e) du mouvement en prenant pour origine la position d'équilibre E de la sphère. On posera 2l=6pRh / m.

Exprimer l'équation horaire du mouvement de la sphère.

projection de la relation fondamentale de la dynamique sur l'axe Oz

Les solutions sont du type :

coefficient de viscosité

On obtient des oscillations amorties de pseudo-période T= 2p / w. Donner l'expression de h en fonction du rayon de la bille, de T₀, et de T.

pseudo période des oscillations amorties T= 2p / w.

période des oscillations non amorties ( dans l'air) : T₀= 2p / w₀.

w²=w₀²-l²

proton dans un champ électrostatique oscillant

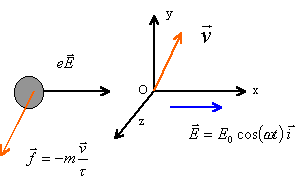
Un proton de masse m et de charge e est soumis à une force de freinage f et à l'action d'un champ électrostatique E variable (voir schéma) . le poids est négligeable.

Ecrire l'équation différentielle où figure la vitesse.

Montrer qu'au bout d'un temps suffisamment long (régime permanent) le mouvement s'effectue suivant ox

relation fondamentale de la dynamique :

résolution de la première équation différentielle du 1^er ordre à coefficients constants avec second membre. La solution est la somme de la solution générale de l'équation sans second membre et d'une solution particulière de l'équation avec second membre.

utiliser les nombres complexes

Montrer que la solution du régime permanent est Vx = V cos(wt + j) où V et j sont des fonctions de w à déterminer.

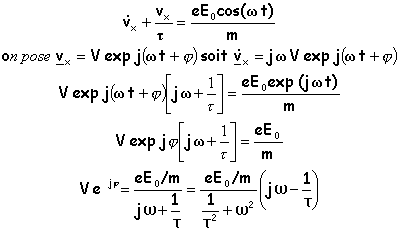
il suffit d'écrire que les modules sont égaux et que les arguments sont égaux.