|
||||
|
théorèmes de la mécanique du solide |
Une navette spatiale de masse m s'approche de la planète Jupiter (centre 0, rayon R = 70000 km, masse M = l,9 1027 kg). Par rapport au référentiel du centre de masse de Jupiter, supposé galiléen, la trajectoire initiale de la navette, loin de la planète, est pratiquement rectiligne, soit x = -Vot, y = b, z= 0 dans un repère (O x y z) convenablement choisi. 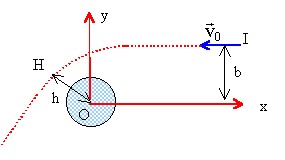 En I survient une panne d'alimentation, qui ne pourra être réparée avant deux jours. Cette panne empêche toute manouvre des moteurs-fusées et toute communication radio. Un appareil de bord indique alors aux trois astronautes leur position I (x = 100 R, y = b = 1, 57 R), et leur vitesse V0 = 50 km/s. Les astronautes rassemblent leurs souvenirs du DEUG et font un petit calcul pour connaître leur trajectoire. Effrayés du résultat, ils décident de lancer un message de détresse dans une "bouteille" qu'ils lanceront dans l'espace. Le problème du mouvement de la navette (inerte) est un problème à deux corps tout à fait analogue à celui de l'expérience de Rutherford. La trajectoire est une branche d'hyperbole de foyer 0, dans le plan xOy, et b s'appelle le paramètre d'impact. La seule différence est qu'il s'agit ici d'une interaction attractive. Si la navette ne percute pas Jupiter, soit H sa position la plus proche du centre OH = h > R.
corrigé |
|||
|
l'énergie potentielle de pesanteur (origine choisie à l'infini) En I : ½ mv0² + GMm/H avec H² = (1,57 R)² + (100 R)² Au regard des valeurs numériques, le terme énergie potentielle est négligeable au point I 6,67 10-11*1,9 1027 m / 7 109 = voisin 1,8 107 m alors que le terme d'énergie cinétique vaut : 1,25 109 m En H : ½ mv² + GMm / h ( G constante de gravitation et h = OH) d'où : v²0 = v² +2GM / h (1)
produit vectoriel rayon vecteur avec la vitesse ou conservation du moment cinétique En I : bv0 en H : hv donc hv= bv0 (2)
éliminer la vitesse de ces deux relations (2) donne : v²=b²v²0 / h² repport dans (1) :v²0 = b²v²0 / h² +2GM / h multiplier par h² et diviser par v²0 : h² =b² + 2r0 h ou h² - 2r0 h - b²=0 résoudre l'équation du second degré en h : D=4 (r0² + b²) h = r0+ racine carrée (r0² + b²) l'autre valeur n'est pas à retenir car h doit être supérieur à R, rayon de la planète application numérique : r0 = 6,67 10-11*1,9 1027 / 25 108 =5,07 107 m. b= 1,57 *7 107 =1,1 108 m racine carrée (r0² + b²) voisin de :1,21 108. h voisin de : 1,7 108 m ( environ 2,4 fois le rayon R soit une altitude voisine de 1,4 R) La bouteille B1 suit la même trajectoire que la navette . Quant aux bouteilles B2 et B3 ,10 m/s est une valeur très faible devant 50 km/s : en conséquence les bouteilles vont suivre à peu près la même trajectoire que la navette. bouteille B2 : en I le produit vectoriel entre le rayon vecteur et le vecteur vitesse s'écrit : 10 x0+bv0 conservation du moment cinétique : 10 x0+bv0 = h1v1. v 1 : vitesse de passage en H l'équation du second degré en h1 s'écrit : h1² - 2r0 h1 -(10 x0/ v0+ b)²=0 bouteille B3 : en I le produit vectoriel entre le rayon vecteur et le vecteur vitesse s'écrit : b(v0-10) conservation du moment cinétique : b(v0-10) = h2v2. v 2 : vitesse de passage en H l'équation du second degré en h2 s'écrit : h2² - 2r0 h2 -b(1-10 / v0 )²= 0
retour - menu |