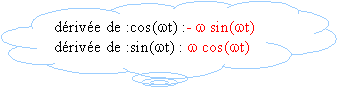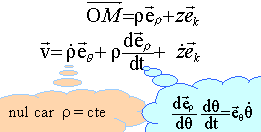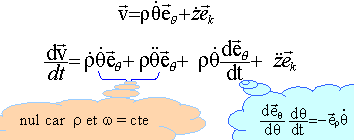|
||||
|
coordonnées cartésiennes, cylindriques. |
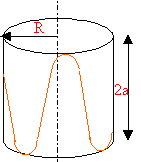
Le manège est constitué d'un disque de centre O tournant autout de l'axe Oz à la vitesse angulaire w constante. Le référentiel d'étude est galiléen. Le cheval de bois M effectue un mouvement vertical suivant l'axe d, d'amplitude a; le mouvement du cheval est périodique : z = a(1+sin(Wt)) 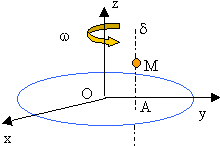
corrigé |
|||
|
x(t) = OA cos(wt) = R cos(wt) y(t) = OA sin(wt) = R sin(wt) z(t) = a(1+sin(Wt)) x² + y² = R² et z² = a²(1+sin(Wt))² OM² = R² + a²(1+sin(Wt))² la trajectoire est représentée ci dessous.
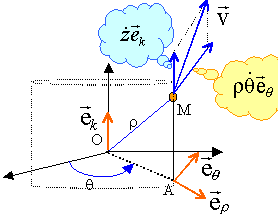
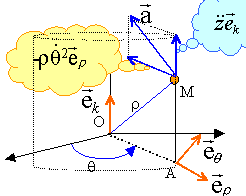
Le vecteur vitesse est la dérivée par rapport au temps du vecteur position:
v² = R²w² + a²W²cos²(Wt) le vecteuraccélération est la dérivée par rapport au temps du vecteur vitesse : x"(t) = -Rw² cos(wt) = - w² x(t) y"(t) = -Rw² sin(wt) = - w² y(t) z"(t) = -aW²sin(Wt) a² = R²w4+ a²W4sin²(Wt) 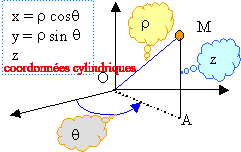
vecteur position : r =R ; q = wt ; z = a(1+sin(Wt)) trajectoire : r =R ; z = a(1+sin(W/w q )) vecteur vitesse : dérivée par rapport au temps du vecteur position
rq ' = rw ; z ' = aW cos(W/w q )); v² = (rw)² + a²W² cos²(W/w q )) vecteur accélération : dérivée du vecteur vitesse par rapport au temps
a² = (Rw²)² + a²W4 sin²(W/w q )
retour - menu |