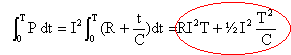Aurélie nov 2001
circuit RL - circuit RC

Google

Une bobine inductive, d'inductance L et de résistance r, est alimentée  :

- en continu: U = 100 V et I = 0,20 A

- en alternatif Ueff = 100 V ; f = 50 Hz ; I eff = 0,196 A

Déterminer r et L.

corrigé
en courant continu, l'inductance n'intervient pas et la bobine se comporte comme une résistance pure en régime permanent

( sauf à la fermeture ou à l'ouverture du circuit où des phénomènes d'induction apparaissent)

100 = r * 0,2 d'où r = 500 W.

en courant alternatif l'impédance de cette bobine est notée Z telle que Z² = r² + (Lw)²

avec Z= Ueff / Ieff = 100/ 0,196 = 510 W.

w= 2p f = 2*3,14*50 = 314 rad/s.

(Lw)²= 510² -500² = 10*(510+500) = 10 100

Lw= 100,5 ohms

L= 100,5 / 314 = 0,32 H.

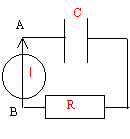Entre le point A et B un générateur de courant idéal débite un courant d'intansité constante I.

  1. Exprimer la tension U(t) aux bornes du condensateur en fonction du temps, et la tension UAB(t) aux bornes du générateur.
  2. Exprimer la puissance électrique fournie par le générateur ( à l'instant t = 0 le condensateur étant déchargé), en fonction de R, I, C, et t.
    - En déduire l'énergie fournie par le générateur pendant l'intervalle de temps [0;T]
corrigé
La loi d'ohm s'écrit : UAB = RI + Uc(t) (1)

I (A) = Q / t avec Q charge d'une armature en coulomb et t en seconde

Q = C Uc(t) avec C capacité en farad

d'où I = C Uc(t) / t

repport dans (1) : UAB = RC Uc(t) / t + Uc(t)

Uc(t)[ 1+RC/t ]=UAB

Uc(t) = UAB / [ 1+ RC / t ].

au bout d'une durée t >> RC le condensateur est chargé et Uc(t) = UAB

La puissance (watt) délivrée par le générateur est la somme de :

la puissance dissipée par effet joule dans la résistance R soit : RI² .

la puissance stockée par le condensateur : P = Uc(t) I

or Q=It et Q=CUc(t)

d'où Uc(t) = I / C t et P = I²/C t

puissance totale : I² (R+ t /C).

énergie mise en jeu durant la durée T :

retour - menu