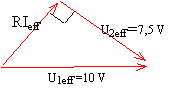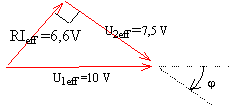Aurélie oct 2001
règles de bases en régime sinusoïdal

nombres complexes et électricité

circuit RC

Google

 

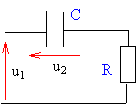u1(t) sinusoïdale de valeur efficace 10 V,de fréquence 1000 Hz ; C = 50 nF ; u2(t) est aux bornes du condensateur.

  1. Quelle est la valeur de R telle que la valeur efficace de u2 soit 7,5 V .
  2. Determiner le déphasage u2 par rapport u1.
  3. Que peut-on dire de U2 eff si la fréquence du générateur devient très grande d'une part et très petite d'autre part.
  4. R et C sont réglables : ils sont ajustés de telle sorte qu'en module, leur impédance totale série reste égale à 5 kW.
    f = 800Hz. Calculer R et C si l'on veut un déphasage de p/6 entre u1 et u2.
    - u2 est elle-en avance ou en retard sur u1?  
corrigé
règle 1 : A chaque grandeur physique, tension, intensité et impédance on associe un nombre complexe:

on peut appliquer à ces nombres complexes, les lois du courant continu.

on utilise toutes les propriétés des nombres complexes vues en maths.

règle 2 : on ne peut pas appliquer les lois du courant continu ni aux tensions efficaces, ni aux intensités efficaces, ni aux normes des impédances complexes.

règle 3 : impédance d'une self pure : jLw; d'un condensateur; -j / (Cw)

Ueff = Z Ieff; relation entre grandeur efficace; Z : norme de l'impédance complexe

pulsation w (rad/s)= 2p fréquence(Hz)

Aux bornes du condensateur la tension est en retard de p /2 par rapport à l'intensité.

appliquer phytagore : (RIeff)² +7,5² = 100 d'où (RIeff)² = 43,75

RIeff = 6,6 V

trouver l'intensité Ieff :

impédance du condensateur : 1/ Cw avec w = 2*3,14*1000 = 6,28 103 rad/s.

et C= 50 10-9 F soit 1/ Cw = 3185 W.

7,5 = 3185 Ieff doù Ieff = 2,35 mA

par suite R= 6,6 / 2,35 10-3 = 2810 W.

u2 en retard sur u1 ::

La phase de la tension u1 est choisie comme origine des phases

tan |j | = 6,6 / 7,5 = 0,88

|j | = 41,3°

u2 en retard de 41,3 ° ou 0,72 rad sur u1.

si la fréquence f du générateur augmente, la pulsation w augmente :

l'impédance du condensateur diminue et va tendre vers zéro : donc u2 tend vers zéro

si la fréquence f du générateur diminue, la pulsation w diminue :

l'impédance du condensateur augmente et va tendre vers l'infini : donc U2eff tend vers 10 V et l'intensité vers zéro.

une lettre soulignée correspond à un nombre complexe

impédance complexe de l'ensemble résistor et condensateur en série : z = R -j / (Cw)

avec w = 2*3,14*800 = 5024 rad/s.

module de z : Z² =R² + (1/(Cw))² = 25 106 (1)

u1 = z i .

arg u1 = 0 pris comme origine

0 = arg z + arg i .

arg z = tan-1 (-1 /(RCw) d'où arg i = tan-1 (1 /(RCw))

d'après le schéma ci-dessus u2 est en retard sur u1.

j est l'angle complémentaire de la phase de i par rapport à u1.

soit RCw = tan p/6 = 0,577 (2)

1 /(Cw) = R/0,577 = 1,732 R repport dans (1) :

R² + (1,732 R)² = 25 106

4 R² = 25 106

R = 2500 W.

C = 0,577/(2500*5024)= 46 nF.

retour - menu