|
nombres complexes et électricité
|
|||
|
On considere le dipôle suivant , la tension efficace est U=220V, de fréquence 50 Hz. 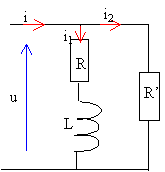 On mesure les intensités efficaces : I=15 A; I1= 8 A; I2= 9 A. Calculer R, R' et L.
corrigé |
|||
|
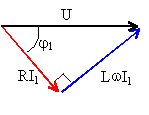
on peut appliquer à ces nombres complexes, les lois du courant continu. on utilise toutes les propriétés des nombres complexes vues en maths. règle 2 : on ne peut pas appliquer les lois du courant continu ni aux tensions efficaces, ni aux intensités efficaces, ni aux normes des impédances complexes. règle 3 : impédance d'une self pure : jLw; d'un condensateur; -j / (Cw) Ueff = Z Ieff; relation entre grandeur efficace; Z : norme de l'impédance complexe pulsation w
(rad/s)= 2p
fréquence(Hz)
Ueff = R' I2 eff R' = 220/9 = 24,5 W. recherche de deux équations à deux inconnues R et L: les nombres complexes associés aux grandeurs physiques sont écrits en bleu, souligné: Ueff = Z1I1 eff d'où Z1 = 220 / 8 = 27,5 W. avec z1 = R+jLw. soit Z1=
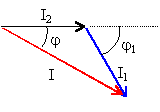
loi des noeuds : i = i1 + i2. les normes de ces trois nombres complexes sont données représenter le triangle correspondant dont on connaît les mesures des trois côtés I, I1 et I2. cela permet de trouver les déphasages entre les courants. prendre la phase de u comme origine des phases. u = R' i2. R' résistance pure donc u et i2en phase.
I² = I2² +I1² - 2I1I2 cos (p-j1)=I2² +I1² + 2I1I2 cos j1. 225=64+81+144cos j1. j1=cos -1 0,555 = 0,982 rad ou - 0,982 rad (-56,25°) or la branche contient une inductance, donc la tension u est en avance sur l'intensité: j1= -56,25°. on trouverait de même : I1² =I² +I2² - 2I I2 cos j j
= cos -1 0,896 =
0,459 rad ou - 0,459 rad (-26,3°)
arg u = 0 = arg z + arg i1d'où arg i1 = -arg z = j1 - tan j1 = -(Lw / R )= -tan 56,25 = -1,496 Lw= 1,496 R (2) calcul de Z : Ueff = Z Ieff d'où Z = 220 / 8 = 27,5 W. repport dans (1) Z² = R² + (Lw)² donne :27,5 ² R² + (1,496 R)² =3,23 R² R = 15,27 W. w = 2*3,14*50 = 314 rad/s. 314 L= 1,496*15,27 L = 72,8 mH.
retour - menu |