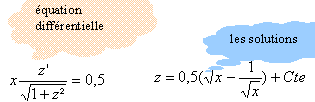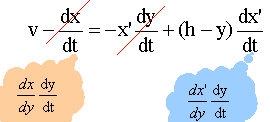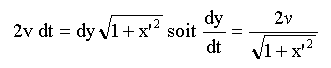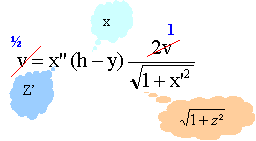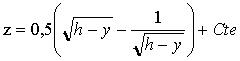|
|||
|
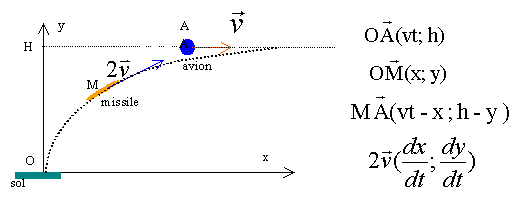
Un avion vole horizontalement à l'altitude h à la vitesse costante notée v. Un missile placé initialement au sol. A l'instant t = 0, l'avion passe à la verticale du missile; le missile décolle en direction de l'avion. la vitesse du misile est le double de celle de l'avion; on suppose que le missile est, à tout instant, dirigé vers l'avion.
corrigé |
|||
|
x(t) = v t z(t) = h = cte trajectoire de l'avion : droite d'équation z = h équations horaires du mouvement du misile :
le vecteur 2v et le vecteur MA sont toujours colinéaires. On note x' = dx / dy vt-x = x' (h-y) dériver cette relation par rapport au temps
v = (h-y) x" dy / dt
(1)
Au cours du temps très petit noté dt, le missile parcourt la distance très petite notée dL à la vitesse 2v. Exprimons de deux manières différentes cette distance dL : dL= 2v dt dL² =dx² + dy² mettre dy² en facteur commun et remplacer dx/ dy par x': dL² =dy²(1+x'²)
repport dans (1) :
On retrouve l'équation différentielle dont on connaît les solutions :
Comment déterminer la constante ? à l'instant t=0, le missile est au sol (y=0) et il est vertical ( x'=z =0) Cte = -0,5( h0,5 -h-0,5 ) ; cette constante sera notée C1. On choisi h comme unité de longueur; alors C1 est nulle. Comment passer de z = x' à x ? On pose Y=h-y La primitive de (Y)½ est : 2/3 (Y)1,5+ cte La primitive de (Y)-0,5 est : 2 (Y)0,5+Cte. d'où la trajectoire du missile : x = 1/3 (Y)1,5 + (Y)0,5 + C2. Comment déterminer C2? à t=0, le missile est en O (0 ; 0) et Y=h C2= -1/3 h1,5 + h 0,5. h étant l'unité de longueur, C2= 2/3. instant de l'impact: Le missile rencontre l'avion lorsque Y = 0. d'une part : ximpact = C2=2/3 d'autre part : ximpact = v timpact timpact = 2 /(3 v ) , h étant l'unité de longueur timpact = 2h /(3v)
retour - menu |