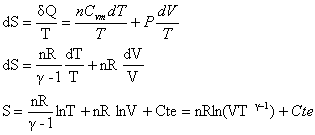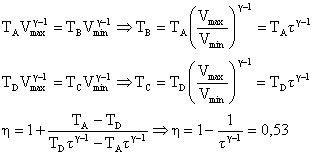|
Capes 96
|
|||
|
Préliminaires:
Etude du moteur : On considère un moteur à combustion interne à allumage par bougies. On se limite à l'étude de l'un des cylindres du moteur. Le cycle thermodynamique décrit par le fluide est le cycle de Beau de Rochas. On en donne la représentation dans un diagramme où l'on porte en ordonnée la pression P du fluide et en abscisse le volume V du gaz contenu dans la chambre du cylindre. Les différente étapes du cycle sont les suivantes: - MA: admission du mélange gazeux air-essence à la pression constante P0. En A il y a fermeture de la soupape d'admission et le volume V est égal à Vmax. - AB : compression supposée isentropique du mélange. Dans l'état B, le volume est égal à Vmin. - BC : échauffement isochore du gaz. CD : détente isentropique du gaz. Dans l'état D le volume est Vmax. DA : refroidissement isochore du gaz. AM : refoulement du gaz vers l'extèrieur, à la pression P0. On convient de nommer "taux de compression" le rapport t =Vmax / Vmin. Le système envisagé est le gaz qui décrit le cycle ABCD. La quantité de gaz n (mol) considérée est celle qui a été admise dans l'état A. Le transfert thermique de l'étape BC est dû à la combustion interne du mélange gazeux admis. Les réactifs et les produits de la réaction sont gazeux. Dans une approche simplifiée on admettra que la quantité de gaz n'est pas modifiée par la combustion interne. Le gaz est assimilé à un gaz parfait pour lequel les capacités thermiques molaires Cpm et Cvm sont constantes. 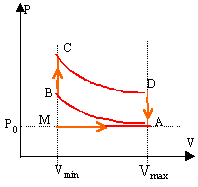
corrigé |
|||
|
Le premier principe traduit la conservation de l'énergie totale d'un système. Soit un système fermé évoluant entre deux état 1 et 2 en recevant de l'extérieur une quantité de chaleur Q et un travail W (grandeurs algébriques), le principe de létat initial permet d'écrire : [W+Q] 1-->2 = E2-E1. où E est l'énergie totale, somme de l'énergie interne U et de l'énergie mécanique( potentielle et cinétique) E=U+Ec+Ep. si l'énergie mécanique ne varie pas : DU=W+Q
P ression en Pa; V volume en m3; n (mol) ; T température en kelvin. énergie interne : DU=W+Q expression différentielle :dU=dW+dQ dU= - P dV + nCvm dT + ldv avec l=P pour ungaz parfait dU=nCvm dT.
S étant constante implique VTg-1=Cte
étape BC: transformation isochore dQ1 = nCvmdT + ldV = nCvm dT Q1 = nCvm(TC-TD). n reste constant alors PB / TB = PC / TC. PC>PB entraîne TC>TB donc Q1 positif, chaleur reçue par le gaz. étape DA: transformation isochore Q2 = nCvm(TA-TD). avec TA<TD donc Q2<0. Au cours d'un cycle l'énergie interne ne varie pas DU=Q1+Q2+W d'où W= -(Q1+Q2). Le rendement est le rapport entre l'énergie mécanique fournie et l'énergie thermique reçue. h = -W / Q1 = (Q1+Q2) / Q1. remplacer Q1 et Q2 par les expressions trouvées ci dessus. h = 1+ (TA-TD) / TC-TB).
d'où : Vmin =Cy / (t-1) = 0,22 L et Vmax = t Cy/ (t-1)= 2,22 L. On détermine la quantité de matière de gaz (mole) entrant dans le cylindre : n = PAVA / (RTA)= 105 * 2,2 10-3 / (8,134*320) = 8,34 10-2 mol or le mélange contient 1 mol
de carburant pour 60 mol de mélange, d'où n'=
n /60 = 1,39
mmol.
Quantité de chaleur Q1 = n'*4,2 106 = 5838 J Q1 = nR (TC-TB) / (g-1) d'où : TC= TB+Q1 (g-1) / (nR) TC= TA tg-1 + Q1 (g-1) / (nR) application numérique : TC=3 463 K. PC = nRTC /
Vmin =10,7
106 Pa.
Q2=nCvm(TA-TD) Q2=nCvm(TA-TC /tg-1 ) Q2= nR / (g-1)[TA-TC /tg-1 ] application numérique : Q2 = -2731 J. Travail fourni au cours d'un cycle : W= -(Q1+Q2) = - 3107 J. Un cycle correspond à deux tours du vilbrequin soit 2000 tours/min. puissance du moteur : 3107*2000 / 60 = 103,6 kW. Pratiquement le rendement est beaucoup plus faible car : - les transformations ne sont pas complétement isochores. -pertes de chaleur à travers les parois. - présence de gaz résiduels - modifications des pressions dues aux soupapes.
retour - menu |