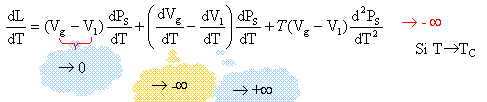Aurélie sept 2001
Equilibre liquide vapeur

Capes interne 91

Google

On s'intéresse à la chaleur latente L de vaporisation en fonction de la température.

  1. Définir chaleur latente molaire de vaporisation de l'eau.
  2. On fait subir à une mole d'eau la transformation EFGHIJE (figure ci-dessous)

    Les volumes molaires de l'eau liquide respectivement aux températures T et T' sont notés Vl et V'l. De même on note Vg et V'g les volumes molaires de la vapeur d'eau aux températures T et T'.On négligera les volumes molaires du liquide face aux volumes molaires de la vapeur. On admettra de plus que la dilatation ou la compression isotherme du liquide s'effectue sans échanges de chaleur avec le milieu extérieur. les capacités calorifiques molaire Cp et Cpg respectivement des phases liquide et vapeur, sont considérées comme indépendantes de la température. On indique que Cp est supérieure à Cpg. La vapeur d'eau est assimilée à un gaz parfait.
    Représenter le cycle étudié sur le diagramme des phases en coordonnées P et T

  3. On appelle L et L' les chaleurs molaires de vaporisation respectivement aux températures T et T'. Appliquer le premier principe de la thermodynamique au cycle considéré et déterminer l'expression de la différence L-L' en fonction de Cp, Cpg, T et T'. En déduire que la chaleur latente de vaporisation peut s'écrire sous la forme L=L0 -aT où L0 et a sont deux constantes positives.
  4. Pour étudier le comportement de la chaleur latente molaire de vaporisation quand la température tend vers la température critique TC on utilise la formule de Clapeyron L= T(Vg-Vl) dPS / dT où PS est la pression de vapeur saturante.
    - Déduire de la formule de Clapeyron les valeurs de limite de L et limite de dL / dT quand T tend vers TC.
    Les dérivée dPS / dT et d²PS / dT² ont des valeurs finies quand T tend vers TC.
    - Tracer l'allure de la courbe de variation de L en fonction de T en utilisant les résultats des questions précédentes.

corrigé

La chaleur latente molaire de vaporisation de l'eau est la quantité de chaleur nécessaire pour faire passer 18 g d'eau (1 mol) de l'état liquide à l'état de vapeur.

D'après le premier principe de la thermodynamique, sur un cycle W+Q=0

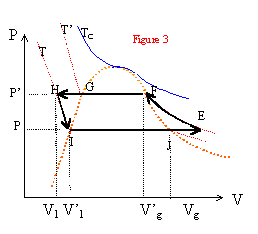
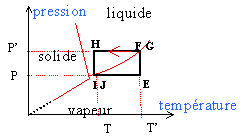
transformation isotherme E--> F : DUEF = 0 = WEF + QEF.

changement d'état F-->G : DUFG = WFG + QFG.

WFG = -P' (V'l-V'g) voisin de P'V'g et QFG = -L'

transformation isobare G-->H : DUGH = WGH + QGH.

WGH = -P' (Vl-V'l) voisin de zéro et QGH = Cp(T-T')

transformation isotherme H--> I : DUHI = 0 = WHI + QHI

changement d'état I-->J : DUIJ = WIJ + QIJ.

WIJ = -P (Vg-Vl) voisin de -PVg et QIJ = L

transformation isobare J-->E : DUJE = WJE + QJE.

WJE = -P (VE-Vg) et QJE = Cpg(T'-T)

la somme des variations d'énergie interne est nulle sur le cycle:

P'V'g -L' + Cp(T-T') -PVg + L-P (VE-Vg)+Cpg(T'-T)=0

utiliser l'équation des gaz parfaits avec n= 1 mole:

L-L' +RT' -RT -RT' +RT + Cp(T-T') +Cpg(T'-T)=0

L-L' = (Cp-Cpg) (T-T').

L=L' + (Cp-Cpg) (T-T').par analogie avec L=L0 -aT

L0 = L' + (Cp-Cpg) T' et a = Cp-Cpg

valeurs limites:

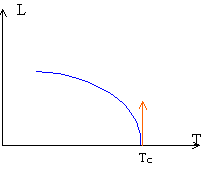
quand T tend vers TC:

le volume du gaz tend vers le volume du liquide: Vg --> Vl et L tend vers zéro.

calculer la dérivée dL/dT :

La dérivée de Vg tend vers l'infini car d'après la figure 3, une légère augmentation de température au voisinage de TC entraîne une diminution de Vg.

par contre une légère augmentation de température entraîne une augmentation de Vl au voisinage de TC: en conséquence la dérivée de Vl tend vers l'infini.

retour - menu