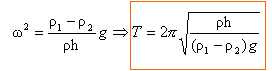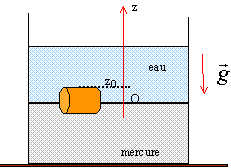
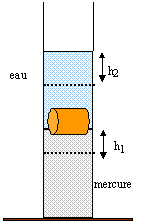Aurélie dec 2001
un objet flotte à la surface de séparation de 2 liquides

 

Google

 

Une éprouvette graduée ( section S) contient du mercure (r1 = 13600 kg/m3) et de l'eau (r2= 1000 kg/m3). Un objet cylindrique ( hauteur h, section s) flotte à la surface de séparation des deux liquides. Le niveau du mercure s'élève de h1 = 80 divisions et le niveau de l'eau s'élève de h2 = 160 divisions.

  1. Calculer la masse volumique r de ce solide homogène.
  2. Même expérience en utilisant un récipient suffisamment large afin que les niveaux des liquides ne change pratiquement pas lors de l'introduction du cylindre. Un dispositif mantient ce solide à la surface de séparation des liquides. Quelle est la hauteur d'immersion dans chaque liquide ?
  3. Le cylindre est légerement écarté de sa position d'équilibre puis abandonné à lui même. Quelle est la période des oscillations ?
corrigé
masse volumique du solide homogène :  

Le volume du cylindre V (m3) est égal au volume de liquide déplacé.

On note u la longueur d'une graduation et S la section de l'éprouvette ( u en mètre et S en m²)

V = u h2 S

volume immergé dans le mercure : V1 = u h1 S

volume immergé dans l'eau : V2 = u (h2 -h1 ) S

le solide est en équilibre sous l'action de la Poussée d'Archimède et du poids du solide: la poussée d'Archimède et le poids du cylindre ont même norme.

Poids : Vr g = u h2 Sr g

Poussée exercée par le mercure : V1 r1 g = u h1 S r1 g

Poussée exercée par l'eau : V2 r2 g = u (h2 -h1 ) S r2 g

u h2 Sr g = u h1 S r1 g + u (h2 -h1 ) S r2 g

simplification par u g S : h2 r = h1 r1 + (h2 -h1 ) r2 .

r = 1 / h2 [h1 r1 + (h2 -h1 ) r2]

calculs : r =1/160 [80*13600+80*1000]= 7 300 kg/m3.

On choisit un axe vertical orienté vers le haut ; l'origine est située à la surface de séparation des liquides.

z0 est l'ordonnée de la partie supérieure du cylindre.

Poids du cylindre : s h r g

Poussée exercée par le mercure : s (h-z0) r1 g

Poussée exercée par l'eau : s z0 r2 g

s h r g = s (h-z0) r1 g + s z0 r2 g

simplification par g s : h r = (h-z0) r1 + z0 r2

h r = h r1- r1 z0 + z0 r2

z0 = h (r1 -r ) / (r2 -r1 ) dans l'eau.

h-z0 = h(r -r2 ) / (r2 -r1 ) dans le mercure.

On note z la position de la partie supérieure du cylindre, à une date t, par rapport à la position d'équilibre.

les lettres écrites en bleu et en gras sont associées à des grandeurs vectorielles.

poids P = s h r g.

poussée : F = s (h-z0 -z) r1 (-g )+ s (z0 +z) r2 (-g).

Dans un référentiel galiléen lié au récipient, la 2ème moi de Newton s'écrit :

s (h-z0 -z) r1 (-g )+ s (z0 +z) r2 (-g) + s h r g = m a. (1)

or à la position d'équilibre (z = 0 )

s (h-z0 ) r1 (-g )+ s (z0 ) r2 (-g) + s h r g = 0.(2)

soustraire (2) de (1) :

s z r1 (-g ) - s z r2 (-g ) = m a.

masse du cylindre : m = shr.

s z r1 (-g ) - s z r2 (-g ) = shr a.

r1z (-g ) - z r2 (-g ) = r a.

projection sur un axe vertical :

r z" + ( r1- r2 ) g z = 0

z" + ( r1- r2 ) g /r z = 0

du type z" + w² z = 0

r1> r2 le mouvement est oscillatoire périodique

retour - menu