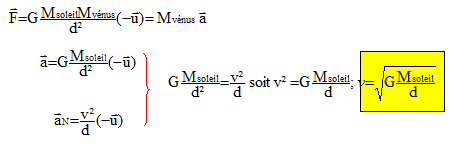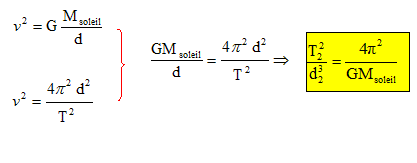Analyse détaillée d'exercices réalisés sous forme de QCM. satellites; lois de Kepler.

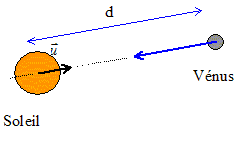
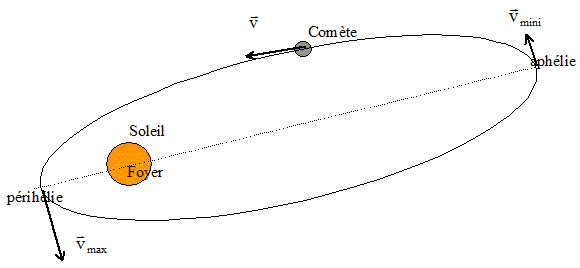
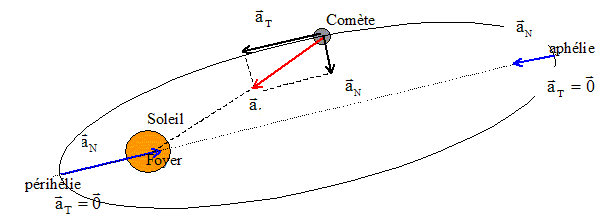
3è loi de Kepler. Texte : référentiel héliocentrique ; le système est Vénus. L'orbite est circulaire. Analyse : Question relative à la vitesse de Vénus. Question relative à la période de Vénus ou de la 3è loi de Kepler. Vénus décrit la circonférence 2pd, à la vitesse v, durant une période T. 2pd = v T     accélération d'une comète. Texte : référentiel héliocentrique ; système : la comète. Analyse : Question relative la vitesse. La conservation du moment cinétique conduit à : Question relative à l'accélération. Question relative à la position du soleil. Le soleil est l'un des foyers de l'ellipse.     Web www.chimix.com satelite géostationnaire. Texte : on admettra qu'un satellite géostationnaire tourne sur une orbite de rayon r =6R0 ( le rayon terrestre est noté R0) Analyse : Question relative à sa position. Un satellite géostationnaire est un satellite qui a une position fixe par rapport au référentiel terrestre ( il reste en permanence à la verticale d’un même point du sol) Pour être géostationnaire le satellite doit avoir: * une trajectoire circulaire de centre O, centre de la Terre * pour période de révolution celle de de la Terre *et de plus il doit tourner dans le même sens que la Terre avec le même axe de rotation donc le plan de sa trajectoire est perpendiculaire à l’axe de rotation de la Terre et il contient le point O : le plan de la trajectoire est obligatoirement équatorial. La masse du satellite n’intervient pas dans l’expression de la période T de révolution du satellite T= 24 h = 86000 s donc R +h a une valeur parfaitement déterminée (h est égale à 36000 km) ; d'après l'expression de la vitesse, celle ci est parfaitement déterminée. Question relative à la relation entre le rayon de l'orbite r et la vitesse de rotation de l'astre central . Hypothèse : l'astre central tourne deux fois plus vite, que devient le rayon de l'orbite géostationnaire ?  3ème loi de Kepler T2/R3=Cte ; de plus T= 2p/w ; si w double alors T est divisée par 2. T2 est divisée par 4 ; donc R3 est divisée par 4 . Le rayon de la nouvelle orbite vaut donc : 6R0/ 41/3 = (6*6*6/4)1/3R0 = 3* 21/3R0. 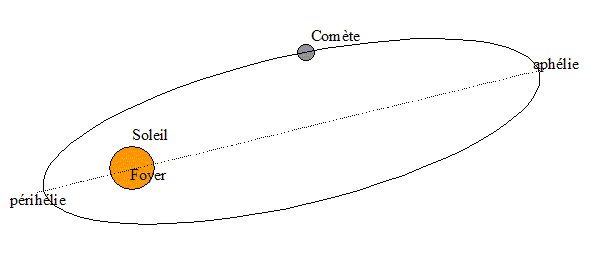Pour propulser une fusée porteuse directement jusqu'à l'orbite géostationnaire du satellite, on procède par transfert d'orbites. Le satellite est d'abord placé sur une orbite basse de rayon r1 puis mené vers l'orbite géostationnaire de rayon r2 à l'aide des moteurs propulseurs. Entre les deux orbites circulaires le satellite emprunte une orbite de transfert elliptique. G est la constante de gravitation, M est la masse de la Terre, m la masse du satellite et r est le rayon de l’orbite. Un satellite géostationnaire est un satellite toujours mobile dans le référentiel terrestre. Faux. Un satellite géostationnaire paraît fixe pour un observateur terrestre. Pour être géostationnaire, il doit graviter autour de la Terre, dans le plan de l’équateur, son sens de rotation étant le même que celui de la Terre sur elle-même et sa vitesse angulaire est la même que celle de la Terre. Vrai. L'énergie cinétique Ec du satellite sur une orbite circulaire de rayon r en fonction de G, M, m et r est : Ec=½mGM/r2. Faux. Ec=½m v2 avec v2 = GM/r. On donne l'expression de l'énergie potentielle gravitationnelle pour le satellite situé à une distance r du centre de la terre, en choisissant l'origine de l'énergie potentielle à l'infini. Ep = - GMm/r. Les moteurs propulseurs doivent fournir le travail moteur W pour que le satellite passe de l'orbite basse de rayon r1 à l'orbite géostationnaire de rayon r2 est : W= GmM(1/r1-1/r2). Faux. Energie mécanique du satellite sur l'orbite de rayon r1 : Ec + Ep =½mGM/r1 -mGM/r1 = -½mGM/r1. Energie mécanique du satellite sur l'orbite de rayon r2 : Ec + Ep =½mGM/r2 -mGM/r2 = -½mGM/r2. la variation de l'énergie mécanique est égale au travail des moteurs : ½mGM/r1-½mGM/r2 =½GmM(1/r1-1/r2).

retour -menu