Analyse détaillée d'exercices réalisés sous forme de QCM. dipôle RLC.

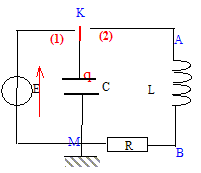
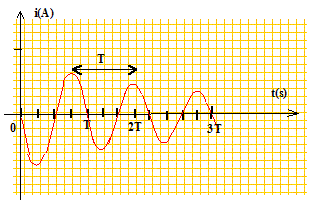
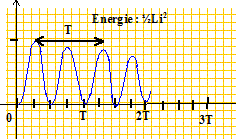
Pseudopériode T. Texte : A la date t=0 le condensateur de capacité C estchargé sous la tension E. On bascule l'interrupteur en position 2. On observe des oscillations pseudopériodiques dans le circuit.   Analyse : Question relative à la pseudopériode. La pseudopériode est la durée séparant deux dates successives où la tension aux bornes du condensateur passe par un extrémum positif. Ce n'est pas la durée séparant deux dates successives où la tension aux bornes du condensateur est nulle.   La pseudopériode est l'intervalle de temps séparant deux dates successives où l'intensité du courant dans le circuit passe par un extrémum positif.  Ce n'est pas l'intervalle de temps séparant deux dates successives où l'énergie emmagasinée dans la bobine est maximale.   dipôle LC. Texte : A la date t=0, le condensateur C2 est chargé ( C1 déchargé) et on bascule l'interrupteur en position 2. On observe des oscillations sinusoïdales libres. Analyse : Question relative à l'expression de la période T. Deux condensateurs en série sont équivalents à un condensateur unique de capacité C=C1C2/(C1+C2). La période est : T=2p (LC)½.     Web www.chimix.com capacité. Texte : un dipôle LC, est formé d'une bobine d'inductance L = 0,50 m H et d'un condensateur de capacité C. La fréquence propre de ce circuit vaut f= 10 MHz. p2 = 10. Analyse : Question relative à la capacité. période T = 1/f = 1/ 107 = 10-7 s. période T = =2p (LC)½ ; T2 = 4p2LC ; C = T2 /( 4p2L) avec L = 5 10-7 H. C= 10-14 /(4*10*5 10-7 )=5 10-10 F. Texte : on charge un condensateur de capacité C= 5mF sous une tension E=12 V. Le condensateur chargé est monté en série avec une bobine d'inductance L et de résistance interne négligeable.L'intensité maximale du courant dans le circuit est 200 mA. Analyse : Question relative à l'inductance. énergie stockée par le condensateur : ½CE² = 0,5*5 10-6 * 122 = 3,6 10-4 J. échange d'énergie entre bobine et condensateur : la bobine peut stockée au maximum ½LI²max d'où L= 2* 3,6 10-4 / 0,22 = 0,018 H = 18 mH. résonance. Texte : un dipôle RLC série est alimenté par une tension sinusoïdale ( valeur efficace constante notée U, fréquence réglable f). On note I l'intensité et Z l'impédance du dipôle. Pour une fréquence particulière f0, on observe que l'intensité efficace passe par une valeur maximale notée I0. Analyse : Question relative à la puissance et à l'énergie. La puissance moyenne consommée par le condensateur est nulle. La puissance moyenne consommée par la bobine ( si sa résistance est voisine de zéro) est nulle. Pour une fréquence quelconque, la puissance moyenne consommée est P= RI2. Autre expression de la puissance consommée : I= U/Z d'où P= R(U/Z)2. Pour une fréquence f0, la puissance consommée est P= RI02. L'intensité étant maximale à la résonance, la puissance consommée est alors maximale.

retour -menu