|
Concours manipulateur électroradiologie médicale Montpellier 2008 Dipôles RC, RL, LC, associations de résistors. |
||||||||
|
||||||||
|
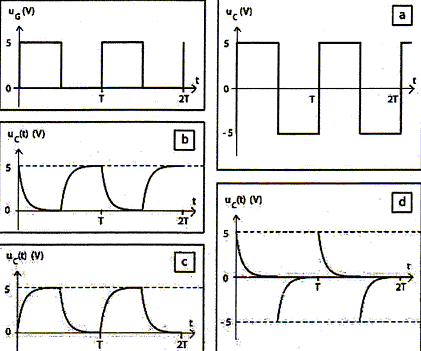
Dipôle RC : Texte : un générateur de tension est associé en série avec un interrupteur, un conducteur ohmique de résistance R et un condensateur de capacité C initialement déchargé. A t=0 on ferme l'interrupteur. Analyse : A t=0, i(0) = 0 : vrai ou faux ? Additivité des tensions : UG= Ri + UC. A t=0, la tension UC (0) est nulle aux bornes du condensateur déchargé. d'où UG= Ri(0) ; i(0) = UG/R, valeur non nulle ( réponse : faux) La tension UG délivrée par le générateur est une tension en crénaux.
Quelle courbe peut représenter la tension uC aux bornes du condensateur ? La tension aux bornes du condensateur est une fonction continue du temps : courbes a et d éliminées. Quand la tension uG aux bornes du générateur est positive, le condensateur se charge et la tension uC à ses bornes est croissante : courbe b éliminée. réponse : courbe c.
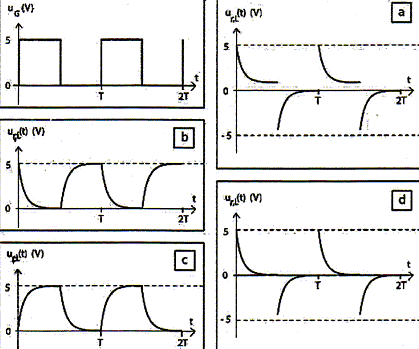
Texte : un
générateur de tension est
associé en série à un
interrupteur, un conducteur ohmique de
résistance R et un bobine d'inductance L, de
résistance interne r non négligeable.
A t=0 on ferme l'interrupteur. Analyse : A t = 0, i(0) = 0 :
vrai ou faux. La bobine inductive introduit un retard à
l'établissement du courant. A l'instant initial, la bobine n'a pas encore eu
le temps de stocker de l'énergie,
½Li2(0) = 0. L n'étant pas nulle, i(0)=0 ;
réponse : vrai.
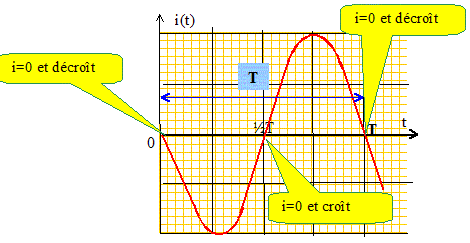
Dipôle LC. Texte : soit un circuit LC, constitué d'une bobine d'inductance L= 0,01 H, de résistance interne négligeable, et d'un condensateur de capacité C = 100 mF, initialement chargé sous une tension E= 10 V. A t=0, on ferme le circuit. Analyse : La période des oscillations de l'intensité du courant circulant dans le circuit est la durée séparant deux dates successives pour lesquelles l'intensité s'annule. Vrai ou faux. Il faudrait ajouter à la phrase précédente " en variant dans le même sens " pour que l'affirmation soit vraie. Réponse : faux.
La période des oscillations de l'énergie emmagasinée par le condensateur vaut, en ms : 0,6 ; 0,003 ; 3 ; 6 ; aucune réponse. Période des oscillations de l'intensité i(t) ou de la charge du condensateur T = 2p(LC)½ avec L = 10-2 H et C = 10-4 F ; (LC)½ =(10-6)½ 10-3. T = 6,3 10-3 s ~ 6 ms. Expression de la charge du condensateur : q(t) = Qmax cos (2pt/T) Expression de l'énergie stockée par le condensateur : ½q2/C. L'énergie est proportionnelle au carré d'un cosinus : la période de cos2 t est la moitié de la période de la fonction cosinus d'où la réponse 3 ms.
Texte : on appelle t1 la date à laquelle, pour la première fois après la fermeture du circuit, l'énergie est répartie de façon égale entre la bobine et le condensateur. On donne racine carrée (0,5) ~ 0,7 Analyse : uC(t1) vaut en V : 10 ; 5 ; 7 ; aucune réponse. Energie maximale stockée par le condensateur : ½CE2 = 0,5*102*10-4 = 5 10-3 J. Expression de la charge du condensateur : q(t) = Qmax cos (2pt/T) avec Qmax = CE =10*10-4 = 10-3 coulomb Expression de l'énergie stockée par le condensateur : ½q2/C= ½ CE2 cos2 (2pt/T). Il faut résoudre : 0,25 CE2 = ½ CE2 cos2 (2pt/T). 1 = 2 cos2 (2pt/T) ; cos2 (2pt/T) = 0,5 ; cos (2pt/T) =+ 0,7 ( 1ère répartition égale) ou -0,7. q(t1) = 0,7 Qmax =0,7 CE soit uC(t1) = 0,7E = 7 V.
La tension aux bornes de la bobine s'annule pour la première fois à la date t2 égale, en ms, à : 12 ; 6,0 ; 3,0 ; 1,5 ; autre réponse. uL = Ldi(t)/dt avec i(t) = dq(t)/dt = -CE(2p/T)sin (2pt/T) di(t)/dt = -CE(2p/T)2cos (2pt/T) Il faut résoudre : cos (2pt2/T) =0 ; 2pt2/T= (2k+1)½ p avec k=0, 1,2 ... t2= 0,25(2k+1)T ; t2=0,25 T avec T = 6 ms ( voir question ci-dessus) ; t2=1,5 ms.
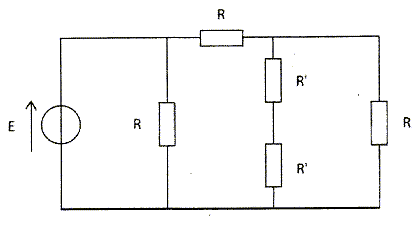
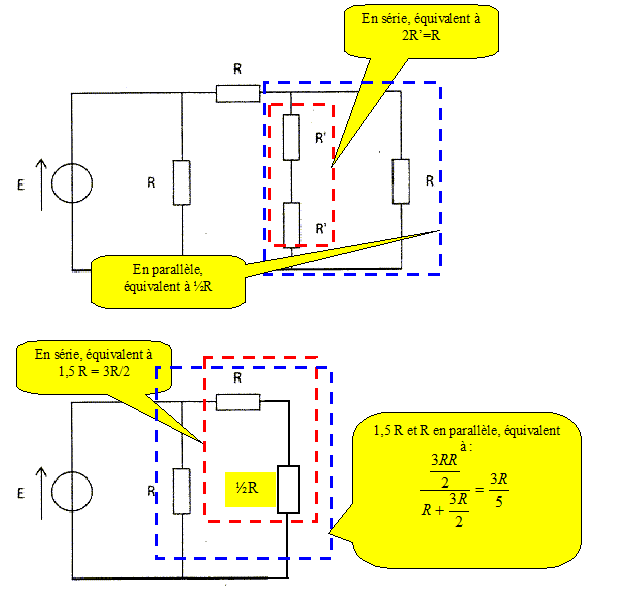
La résistance équivalente du circuit vaut 5/8R ; 5/3 R ; 4R ; autre réponse. Donnée : R'=½R.
E= 12 V ; R=50 W. L'intensité du courant circulant dans le circuit est :4 A ; 0,14 A ; 0,4 A ; autre réponse. I= E / Réquivalent = E*5/(3R) =12*5/(3*50) =0,4 A. |
||||||||
|
|
||||||||
|
|