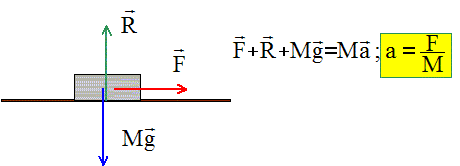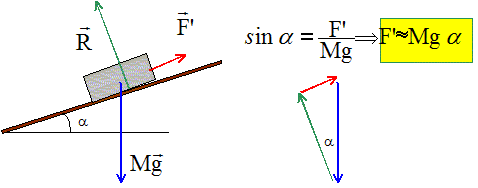Analyse détaillée d'exercices réalisés sous forme de QCM. cinématique, travail, énergie, accélération.

Cinématique. Texte : une voiture est stationnée à d=90 m d’un piéton immobile. A un instant donné elle démarre et roule avec une accélération constante de a=5 m.s-2. On prendra 5½~2,24 Elle passe devant le piéton après 10 s. Faux. Distance parcourue par la voiture d'un mouvement rectiligne uniformément accéléré. x(t) = ½at2 ; t =[2d/a]½ = [2*90/5]½ = [36]½ = 6 s. Une seconde voiture part du même endroit avec une accélération constante mais met le double de temps pour atteindre l’individu. L’accélération de ce second véhicule est de 2,5 m.s-2. Faux. a =2d / t2 =2*90/122 =20*9/144 = 20/16 = 1,25 m s-2. L’individu jusque là immobile se met à se courir et ses coordonnées en mètres par rapport à un repère orthonormé sont : x(t) = -0,5 t2+5t+30 ; y(t) = 0,25 t2-10t +30. La vitesse de cet individu après 10 s est de l'ordre de 7 m/s. Vrai. La vitesse est la dérivée de la position par rapport au temps. x'(t) = -t+5 ; y'(t) = 0,5t-10 x'(10) = 5 m/s ; y'(10) = -5 ; v=[52 +(-5)2]½ = 50½ ~ 7 m/s. Son accélération après 10 s est de 1,12 m/s2. Vrai. Dériver les expressions de la vitesse par rapport au temps : x"(t) = -1 , y"(t) = 0,5 ; a = [0,52 +(-1)2]½ = 1,25½ = (5*0,25)½~2,24*0,5 = 1,12 m/s2. Travail. Texte : On souhaite transporter un objet M=50 kg de l’entrée d’une boutique à une voiture stationnée dans un parking situé un peu loin. La vitesse de déplacement est de 2 km/h. Lorsque l’on pousse l’objet sur le sol, il est soumis à une force de frottement dynamique de module f= µmg avec µ =0,75 coefficient de frottement dynamique. Une personne transportant cet objet, durant les 10 minutes nécessaires pour arriver à la voiture, fourni un travail nul. Vrai. Pour porter la valise, la force musculaire motrice est opposée au poids de l'objet. Cette force est verticale et le déplacement est horizontal : une force perpendiculaire au déplacement ne travaille pas. Il est plus facile de porter cet objet que de le pousser. Dans l'hypothèse ou " plus facile " signifie le travail mécanique est plus petit : Le travail de la force musculaire est l'opposé du travail de la force de frottement W = µmg d avec d = 2000/60*10 = 2000/6 ~330 m et µmg =0,75*50*10 = 375 N W = 375*330 ~1,2 105 J. Dans l'hypothèse ou " plus facile " signifie la fatique est plus faible : Vrai. Le mouvement du centre de masse du porteur en marchant est un mouvement accéléré et freiné à chaque pas, ce qui dissipe l’énergie et explique la fatigue quand on porte l’objet. Vrai. L’objet est au 3ème étage de la boutique qui n’a pas d’ascenseur. La hauteur de chaque étage est estimée à 3 mètres. L’énergie potentielle acquise par l’objet est de l’ordre de 6 kJ. Faux. Ep=mgh = 50*10*9 = 4500 J = 4,5 kJ.   Texte : une voiture d’une tonne se déplace horizontalement suivant un axe Ox. Elle démarre à l’instant t=0 à partir du point O et met 20 secondes pour parcourir 1 km. L’action du moteur est assimilable à une force motrice F. On prendra g=10 m.s-2. Le mouvement de cette voiture est x(t) = F/M t2. Faux. x(t) = ½F/M t2. La force motrice a pour module 600 N. Faux. F = 2x M/t2 = 2000*1000/202 =100*1000/20=5000 N. Au bout des 20 secondes, la voiture aborde une pente de 10%. On souhaite que la voiture grimpe à vitesse constante avec une force de traction notée F'. On considèrera dans cet exercice que les angles sont petits ce qui permet de faire l’approximation des petits angles tan a ~ sin a~a. F'=1000 N. Vrai. Dans un mouvement rectiligne uniforme la somme vectorielle des forces est nulle. F' = 1000*10*0,1 = 1000 N. Arrivée au sommet de cette pente, le conducteur aperçoit un obstacle à une distance de 100 mètres. La valeur de la décélération minimale qu’il doit imposer à la voiture s’il souhaite s’arrêter sans choc est 5 m.s-2. Faux. La variation d'énergie cinétique est égale à la somme des travaux des forces. 0-½Mv2 = Ma' d avec d = 100 m. a' = -0,5v2 /d. Quand à la vitesse v : a = F/M = 5000/1000 = 5 m s-2 ; v = at = 5*20 = 100 m/s. ( valeur peu réaliste) a' = = -0,5*1002/100 = -50 m/s2.     Web www.chimix.com Energies. On abandonne sans vitesse initiale un bloc de masse m à partir du sommet d'un plan incliné faisant un angle q avec l'horizontale. On prendra Oz comme axe vertical ascendant perpendiculaire au plan incliné et l'axe Ox orienté suivant le plan incliné. Le bloc glisse sans frottement et vient comprimer un ressort de constante de raideur k en bas du plan incliné. L'origine des énergies potentielles est prise à la position initiale de la masse. Au moment du choc, le ressort est comprimé d'une longueur d avant de se détendre à nouveau et toute l'énergie cinétique est transformée en énergie potentielle. L’énergie potentielle de pesanteur du bloc (avant le choc) est : Ep = -mgx sin q. Vrai. Altitude avant le choc : - x sinq ; x est la distance parcourue sur le plan incliné. énergie potentielle avant le choc : Ep = -mgx sin q. La variation d'énergie cinétique entre l'instant où le ressort initial et l'instant où le ressort est totalement comprimé est nulle. Vrai. La vitesse initiale étant nulle, l'énergie cinétique initiale est nulle. A l'instant où le ressort est entirement comprimé, la masse m est immobile, sa vitesse est nulle. La constante de raideur du ressort est k = 2mg sin q [(L+d)/d2]. Vrai. On considère le système { masse - ressort } A l'instant initial l'énergie mécanique est nulle. A l'instant où le ressort est entièrement comprimé l'énergie mécanique est sous forme potentielle : ½k d2 - mg(L+d) sin q. L'énergie mécanique se conserve en absence de frottement : ½k d2 - mg(L+d) sin q. k = 2mg sin q [(L+d)/d2]. Le bloc va remonter jusqu' à moitié de sa position initiale. Faux. L'énergie mécanique se conserve en absence de frottement : le bloc remontera jusqu' à sa position initiale. 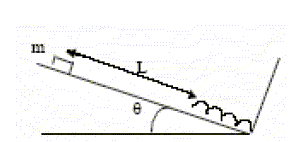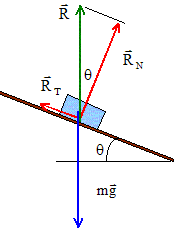Une benne transporte un objet de masse m positionné comme indiqué sur la figure ci-dessous. La benne se soulève à vitesse constante et au bout de 30 secondes, l'objet se met à glisser et le chauffeur arrête immédiatement la benne. L'angle entre le plancher de la benne et l'horizontal est alors q= 30�°. sin30=0,5 ; cos30~0,8 ; tan30~0,5 ; g= 10 m.s-2. La force de frottement statique quand elle est maximale s'exprime f max =mR, R réaction entre le plancher et l'objet. Le coefficient de frottement statique entre le plancher de la benne et l’objet est mstat~0,5. Vrai. Juste avant de glisser, l'objet est en équilibre sous l'action de son poids et de l'action du plan : ces deux forces sont opposées et ont même valeur. mstat =tan q = RT/RN =tan 30 = ~0,5. L'objet ne s'arrête pas et glisse avec une accélération uniforme et se déplace de 2 m en 2 s jusqu'au bout de la benne fermée. Cette accélération est due à la différence entre la gravitation et la force de frottement dynamique qui s'exprime fdyn =mdyn R. L’accélération de l’objet est de 3 m.s-2. Faux. Mouvement uniformément accéléré avec vitesse initiale nulle : x(t) = ½at2 soit a = 2x(t) / t2 = 2*2/22=1 m s-2. Le coefficient de frottement dynamique lors de l’accélération de l’objet est (gsinq-a) / (gcosq). Vrai. Ecrire la seconde loi de Newton : - sur un axe parallèle au plan orienté vers le bas : mg sin q -RT = ma ; RT =m(g sin q-a) - sur un axe perpendiculaire au plan : -mg cos q +RN=0 ; RN=mg cos q mdyn =RT /RN=(gsinq-a) / (gcosq). Le coefficient de frottement dynamique lors de l'accélération de l'objet est 1,5. Faux. mdyn =(10*0,5-1) / (10*0,8) = 4/8 = 0,5. Un ascenseur, dont la hauteur entre le plancher et le plafond est de h=2,2 m, démarre à l’instant initial pour monter avec une accélération constante a = 1,2m.s-2. On prendra l’axe des z comme axe ascendant. A la date t=3 s, une araignée maladroite se détache du plafond. On prend g=10 m.s-². Le mouvement de l’araignée dans le référentiel lié à l’ascenseur peut être obtenu à partir de l’équation suivante d2z/dt2=-g-a. On peut déterminer à partir de l’instant initial : La vitesse de chute de l’araignée par rapport au plancher P de l’ascenseur de cote nulle est : dz/dt=-(g+a)(t-3). Vrai. La vitesse est une primitive de l'accélération : dz/dt = -(g+a) (t-3) + Cte La vitesse initiale de chute est nulle : Cte =0. La position de l’araignée par rapport au plancher P de l’ascenseur de cote nulle est : z(t) = -½(g+a) (t-3)2+h pout t<= 3s. Faux. Il faudrait écrire pout t >= 3 s. Pour t compris entre 0 et 3 s, l'araignée est immobile à 2,2 m au dessus du plancher. La position Z(t) de l’araignée par rapport au fond O du puits de l’ascenseur de cote nulle est : Vrai. Z(t)= -½g(t-3)2+3,6(t-3)+7,6 pour t >=3 s Z(t) = ½at2+h pour t compris entre 0 et 3 s. Le référentiel terrestre est supposé galiléen. Avant sa chute l'araignée a le même mouvement que l'ascenseur ; l'araignée est immobile à l'altitude initiale h. Z(t) = ½at2+h pour t compris entre 0 et 3 s. Lors de sa chute l'araignée est soumise à son poids ; sa vitesse initiale est la vitesse de l'ascenseur à t=3 s soit : v(t) = at = 1,2*3 = 3,6 m/s. La position de l'araignée est à t=3 s : Z(3) = ½*1,2*9+2,2 = 7,6 m. Z(t)= -½g(t-3)2+3,6(t-3)+7,6 pour t >=3 s La chute libre de l’araignée dure 5 secondes. Faux. Lorsque l'araignée est sur le plancher de l'ascenseur, l'altitude du fond de l'ascenseur et l'altitude de l'araignée sont identiques. Position du plancher de l'ascenseur à t= 3+5 =8 s : Z(8)= 0,6*64 = 38,4 m ; Position de l'araignée t=5 s : Z(8) = -5*25+3,6*5+7,6 = -99,4 m. Calcul de la date t : -½g(t-3)2+3,6(t-3)+7,6 = ½at2. -5(t-3)2 + 3,6(t-3)+7,6 = 0,6 t2 ; -5t2 +30t-45 +3,6 t-10,8 +7,6 = 0,6t2. 5,6t2 -33,6 t +48,2=0 ; D½=7,02 ; t=3,63 s. durée de la chute : 0,63 s.

retour -menu