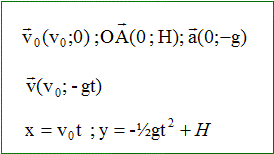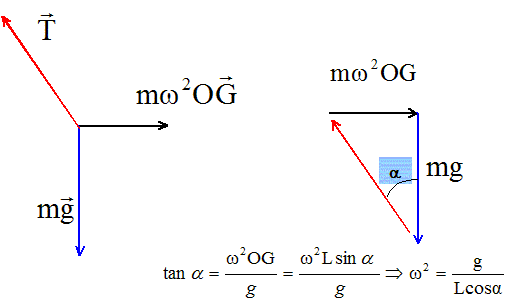
Analyse détaillée d'exercices réalisés sous forme de QCM. Forces : Laplace, Archimède, force d'inertie centrifuge, accélération.

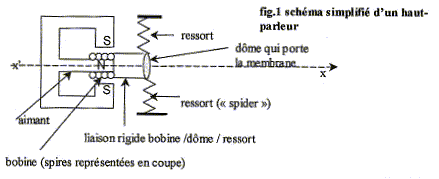
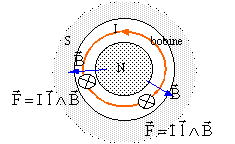
Haut parleur et force de Laplace : Texte : La bobine susceptible de se déplacer, traversée par un courant I, placée dans un champ magnétique B, est soumise aux forces de Laplace. Le forces de Laplace sont verticales, vers le bas.( vers le haut, si I change de sens) Analyse : Quelle est la longueur du fil de la bobine ? On donne : N= 50 spires de rayon 2,0 cm = 0,020 m. Longueur d'une spire = circonférence du cercle de rayon R = 2pR. Longueur des 50 spires : L = 2*50 p R =314*0,02 = 6,3 m. Quelle est la valeur de la force de Laplace ? On donne : B=250 mT = 0,25 T et I = 200 mA = 0,2 A. F= B I L = 0,25*6,3*0,2 = 0,315 N. Quelle est la puissance de la force de Laplace ? On donne : la bobine se déplace de 8 mm en 10 ms. Vitesse de la bobine : 8/10 = 0,8 m/s. Puissance (W) = force (N) * vitesse (m/s) = 0,315*0,8 =0,25 W. Chute dans un liquide. 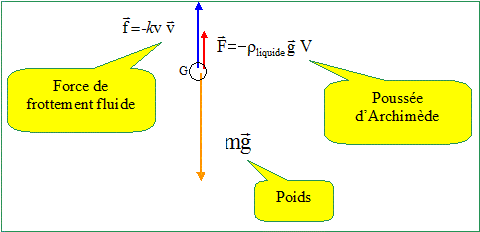Texte : La bille : masse m ; diamètre D=2R, masse volumique r. Analyse : Question relative à la masse de la bille. masse (kg)= masse volumique (kg m-3) * volume (m-3). Volume d'une sphère V = 4/3pR3=1/6pD3. m = r V ; V= m / r. Question relative à l'expression de la vitesse limite vlim. Lorsque la vitesse limite est atteinte, le mouvement est rectiligne uniforme. D'après le principe d'inertie, les forces se neutralisent : mg = rliq gV + kv2lim ; mg = mg rliq / r + kv2lim ; kv2lim = mg(1-rliq / r) ; v2lim = mg/ k (1-rliq / r).   Rotation et force d'inertie centrifuge. Texte : le solide de masse m= 100 g tourne à vitesse angulaire constante w autour d'un axe vertical. Analyse : Question relative à la valeur minimale de w permettant à la bille de décoller de l'axe ( a >0). On se place dans un référentiel lié à la bille G. Dans ce référentiel, la bille est immobile. Elle est soumise à son poids ( valeur mg), à la tension du fil et à une force d'inertie centrifuge ( valeur mw2OG). Au moment où la bille quitte la verticale a~0 ; cos a ~1 et w =(g/L)½ =(9,8/0,5)½ =4,4 rad/s. Question relative à la valeur minimale de w telle que le fil BG soit tendu. Dans ce cas cos a = d/L = 0,4/0,5 =0,8 et w =(g/Lcos a )½ =(9,8/0,4)½ =4,9 rad/s.     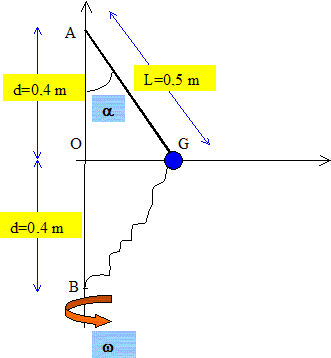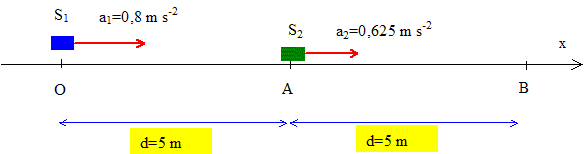Web www.chimix.com Deux véhicules sur une même route. Texte : S2 démare avec un retard q sur S1 ; S1 démarre à une date choisie comme origine. S1 rejoint S2 en B. 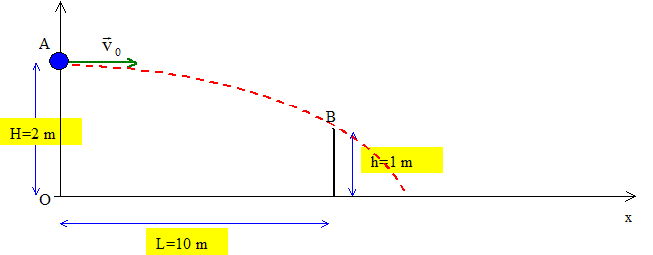Analyse : Question relative à la durée du parcours OB.  x1 = ½a1t2 = 0,5*0,8 t2 = 0,4 t2. Durée du parcours OB : t2 =10/0,4 =25 ; t = 5 s. Question relative au retard q. x2 = ½a2(t-q)2 +OA = 0,5*0,625(t-q)2 +5 Durée du parcours AB : (t-q)2 =10/0,625 =16 ; t-q= 4 ; q = 1 s. Projectile : Texte : On néglige les frottements. g~ 10 m s-2. Analyse : Question relative à la vitesse v0 telle que la balle passe en B. yB = h= -½gt2B +H ; t2B =2(H-h)/g=2/10= 0,2 ; tB=0,45 s  xB = L = v0tB ; v0 = L/ tB= 10/0,45 = 22 m/s.

retour -menu