Concours Esiee : 4 années de QCM bobine inductive, dipôle RL

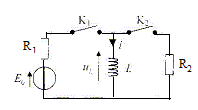
Le générateur délivre une tension constante E0 et la bobine est parfaite. Les résistances R1 et R2 sont différentes. De t=0 à T K1 est fermé et K2 est ouvert. T est suffisamment long pour "charger" complètement la bobine. A- L'intensité initiale est nulle. Vrai. La bobine s'oppose à l'établissement du courant à la fermeture de K1. B- La tenion finale aux bornes de la bobine est nulle. Vrai. uL= Ldi/dt ; uL(T) = L[di/dt ]T ; en régime permanent [di/dt ]T =0. A partir de t=T, K1 est ouvert et K2 est fermé. C- L'intensité à la date t = T+est nulle. Faux. A t =T+ , I(T)=I(T+)= E0/R1. Continuité de l'intensité. D- La tension aux bornes de la bobine est nulle à la date t=T+. Faux. Discontinuité de la tension aux bornes de la bobine : uL(T+) + R2I(T+) = 0 ; uL(T+) =- R2I(T+) = - R2E0/R1.   E-La constante de temps du circuit entre [0 ; T) est la même qu'à t >T . Faux. t1 = L/R1 et t2 = L/R2 avec R1différent de R2.   Le générateur délivre une tension constante E0 =4 V et la bobine est parfaite. L= 10 mH ; R1 =10 W ; R2 =20 W. De t=0 à T=10 ms K1 est fermé et K2 est ouvert. T est suffisamment long pour "charger" complètement la bobine.  A- L'énergie accumulée par la bobine à t=T- est 8 10-4 J. Vrai. Le régime permanent est établi et I = E0/R1 = 4/10 = 0,4 A ½LI2 = 0,5*0,01*0,42 = 8 10-4 J B- L'énergie dissipée dans R1 de t=0 à T vaut 8 10-4 J. Faux. Energie dissipée par effet Joule dans R1 pendant la durée dt : dW =R1i2dt avec i = E0/R1(1- exp(-t/t)) ; t = L/R1 = 10-3 s ; T= 10t. dW= R1(E0/R1)2(1- exp(-t/t))2dt = R1(E0/R1)2[dt + exp(-2t/t)dt -2exp(-t/t)dt] intégrer entre 0 et 10t : E02/R1 [t + (-½ t ) exp(-2t/t)+ 2t exp(-t/t)]010t =E02/R1 [10 t+½ t -2 t]010 t. E02/R1 (8,5 t ) = 16/10 * 8,5 10-3 = 136 10-4 J. C- L'énergie fournie par le générateur de t=0 à T vaut 16 10-4 J. Faux. Energie fournie par le générateur pendant la durée dt : dW =E0idt avec i = E0/R1(1- exp(-t/t)) dW = E02/R1(1- exp(-t/t))dt intégrer entre 0 et 10t : E02/R1 [t +t exp(-t/t)]010 t = E02/R1 (10 t-t ) = E02/R1 (9t )= 16/10*9 10-3 = 144 10-4 J. A partir de t=T, K1 est ouvert et K2 est fermé. D-L'énergie accumulée par la bobine à t = T+ est 2 10-4 J. Faux. L'énergie stockée à la date t=T est identique à l'énergie stockée à la date t=T+. E-L'énergie dissipée par effet joule à travers R2 vaut 2 10-4 J. Faux. Elle est égale à l'énergie stockée à t=T+ par la bobine soit 8 10-4 J.     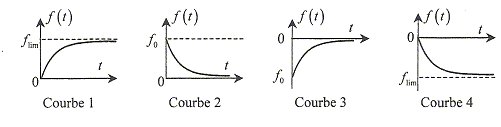Web www.chimix.com Le circuit RL est alimenté par un générateur de tension constante E0. 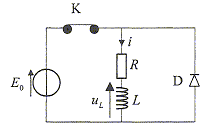Lors de l'établissement du courant ( K fermé) A- Le courant i à l'allure de la courbe 1. vrai B-La tension uL à l'allure de la courbe 2.vrai Lors de l'interruption du courant ( K ouvert) C- Le courant i à l'allure de la courbe 3 faux Continuité de l'intensité, donc courbe 2 D- La tension uL à l'allure de la courbe 4. faux Discontinuité de la tension uL, donc courbe 3 E- La tension aux bornes de R a toujours la même allure que i. vrai intensité qui traverse le résistor et tension aux bornes du résistor sont proportionnelles. 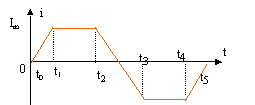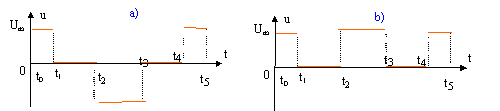Le courant circulant à travers une bobine parfaite d'inductance L évolue en fonction du temps t comme indiqué ci-dessous : La tension UL(t) aux bornes de la bobine est de la forme : tension aux bornes de la bobine : U= Ldi/dt entre t2 et t3 : di/dt est négative , L est positive donc U<0 a )vrai ;b) faux c) entre t0 et t1 la bobine fonctionne en mode générateur d) entre t4 et t5 la bobine fonctionne en mode générateur entre t0 et t1 la bobine stocke de l'énergie et fonctionne en mode récepteur c) faux entre t4 et t5 la bobine stocke de l'énergie et fonctionne en mode récepteur d) faux. e) L'énergie accumulée par la bobine de t0 à t1 vaut UmIm( t1-t0)/2. énergie stockée : dE= u i dt = L i di puis intégrer de t0 à t1 : E= ½LI²m Or i = kt ( k = constante) ; Um= Ldi/dt = Lk ; Im = kt1 ; t1 = t1-t0 car t0=0. E= ½L( kt1)2=½Lk * kt1*t1 = ½UmIm( t1-t0) e )vrai

retour -menu