Concours Esiee : 4 années de QCM réflexion, réfraction.

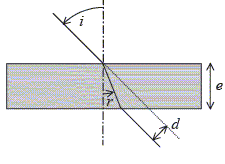
Un rayon monochromatique arrive sur une lame à face parallèle avec un angle d'incidence i. On note n l'indice de la lame, e son épaisseur, r l'angle du rayon réfracté et d la déviation en sortie de la lame. l'indice de l'air vaut 1. A- Pour n=1,4 et i = 45°, r est de l'ordre de 30°. Vrai. loi de Descartes pour la réfraction : nair sin i = n sin r ; sin 45 = 1,4 sin r ; sin r = 0,7 / 1,4 = 0,5. B- Pour n>1,4 et i = 45°, r >30° . Faux. sin r = 0,7 / n ; si n augmente alors sin r diminue ; r diminue. C-Pour n=1,4 eti<45° alors r<30°. Vrai. sin r = sin i / 1,4 ; si i diminue, sin i diminue et r diminue.   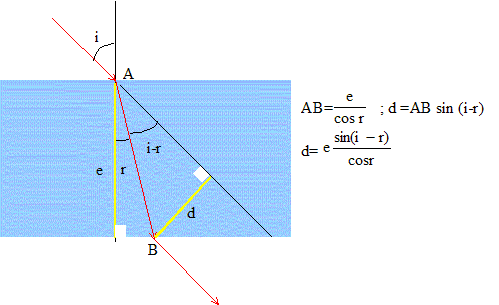D- d = e sin ( i-r). Faux.   E- d = e tan r. Faux.   Un faisceau lumineux incident traverse en H et K un prisme équilatéral. Lorsque iH= 45 ° le faisceau HK est horizontal. L'indice de l'air est égal à 1. A. l'indice du prisme vaut 1,3. faux. Loi de Descartes pour la réfraction en H : sin 45 = n sin rH avec rH = 30° ; sin 30 = 0,5 n = 0,707/0,5 =1,41. B. pour iH=45°, le rayon sortant en K et le rayon incident ont la même direction. faux. Loi de Descartes pour la réfraction en K : n sin 30 = sin rK par suite iK=45°. C. pour iH = 40,5°, rH~30°.faux. D. pour iH = 90°, rH~45°. vrai. Loi de Descartes pour la réfraction en H : sin 90 = 1,41 sin rH ; sin rH = 1/1,41 = 0,707 ; rH~45°. E. il existe un angle iH pour lequel on observe aucune réfraction. faux. Cela ne peut pas se produit quand on passe de l'air dans un verre, milieu plus réfringent que l'air.       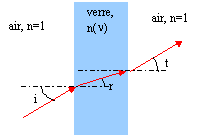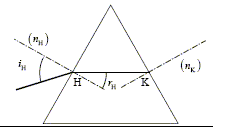Web www.chimix.com S   Une onde lumineuse de longueur d'onde l dans le vide traverse une lame de verre dont l'indice n dépend de l suivant la loi de Cauchy n= 1,619 + 0,0102/l² où l s'exprime en mm. Les fréquences des radiations violettes et rouge dans l'air ( assimilé au vide) valent nviolet= 7,5 1014 Hz et nrouge= 3,75 1014 Hz. 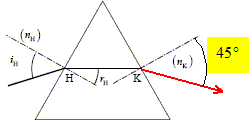Quand i(lrouge) = i(lviolet) a) r(lrouge) >r(lviolet) b) r(lrouge) <r(lviolet) c) t(lrouge) >t(lviolet) sin i = n sin r ; sin r = sin i / n ; lviolet<lrouge donc n violet > n rouge donc r(lrouge) >r(lviolet) a) vrai et b) faux d) Dans le verre la lumière violette se propage moins vite que la lumière rouge. e) Quelle que soit la longueur d'onde, i(l)= t(l). Dans la lame de verre, quelle que soit la longueur d'onde, i(l)= t(l) donc e) vrai ; c) faux réfraction sur le premier dioptre : sin i = n sin r réfraction sur le seconde dioptre : n sin r = sin t d'où i = t célérité dans le verre = c/ n ; or n violet > n rouge donc v violet <vrouge. d) vrai .   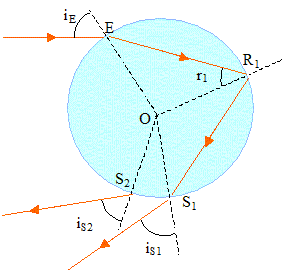La goutte d'eau est supposée sphérique. Sur le schéma figurent la trajectoire de la lumière de longueur d'onde l1 ( réfraction suivant ER1, puis réflexion suivant R1S1, réfraction en S1 et sortie sous l'angle iS1) et le rayon émergeant en S2 avec un agle iS2 correspondant à une longueur d'onde l2. L'indice de l'eau est une fonction décroissante de la longueur d'onde. nair = 1. l1 est-elle inférieure à l2 ? iS1 est-il égal à iSE ? iS1 est-il égal à iS2 ? On donne la célérité c de la lumière dans le vide et les fréquences nviolet et nrouge des radiations violette et rouge dans l'air : c = 3 108 m/s ; nviolet =7,5 108 MHz ; nrouge =3,75 108 MHz . - lviolet vaut-elle 400 nm ? - Dans un arc en ciel simple, l'arc rouge est-il au dessus du violet ?  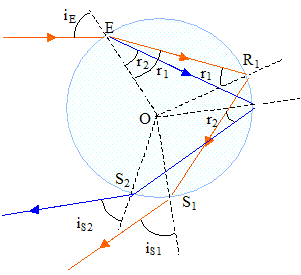réfraction en E : pour la radiation de longueur d'onde l1 : nair sin iE = n1 sin r1 ; pour la radiation de longueur d'onde l2 : nair sin iE = n2 sin r2 ; n1 sin r1 = n2 sin r2 ; Dans l'hypothèse "l1 est inférieure à l2 " : n1 < n2 et donc sin r1 >sin r2 ; r1 > r2 .   réfraction en S1 : n1 sin r1 = nair sin iS1. Or nair sin iE = n1 sin r1 d'où : iS1 = iE. réfraction en S2 : n2 sin r2 = nair sin iS2. Or nair sin iE = n2 sin r2 d'où : iS2 = iE = iS1. lviolet = c/ nviolet =3 108 / 7,5 1014 =4 10-7 m = 400 nm Dans un arc en ciel simple, l'arc rouge est dessus du violet.

retour -menu