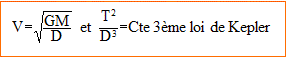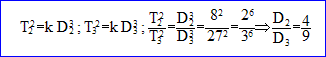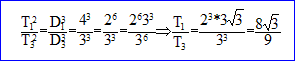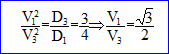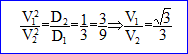Concours Esiee : 4 années de QCM satellite, lois de Kepler.

P-a, P-b, P-c sont trois planètes satellites d'un astre A.Leur orbite est circulaire. Le tableau ci-dessous donne certaines valeurs approchées des grandeurs suivantes : - R et M, respectivement le rayon et la masse des planètes ou de l'astre, supposés sphériques homogènes. - Le champ de gravitation à la surface de ces corps. - T et d, respectivement la période de révolution et le rayon des orbites des planètes autour de A. Les planètes n'interagissent pas entre elles. R(m) M(kg) g(m/s²) T(s) d(m) P-a 2 107/3 2 1025/3 1,5 1011 P-b 3 1027 5/4 4 *3½ 108 P-c 107/3 1024/3 2 9 *2½ 1011/2 3 1031/3 A 2 109/3 1,5 105 xxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxx A- R(P-b) = 4 108 m. Vrai. gB= MBG/RB2 ; RB2 =MBG/gB=3 1027*6,67 10-11 *4/5 =3*6,67*4 1016 /5 =16 1016 ; RB =4 108 m. B- M(A) = 1031 kg. Vrai. 3éme loi de Kepler : T2/d3 = 4p2/(GM) ; dans le cas de P-c : T2/d3 =81*2 1011 / 27 1031 =6 10-20. 4p2/(GM) = 6 10-20 soit M = 4p2/(G*6 10-20 )= 4*10 / (6,67 10-11 * 6 10-20 ) = 40 1031 / (6,67*6) = 1031 kg. C- g à la surface de P-a vaut 10 m/s². Vrai. D- T(P-a) = 45 1011/2 s. Vrai. dans le cas de P-a : T2/d3 =6 10-20 ; T2= 6 10-20 * d3 = 6 10-20 *(1,5 1011)3=9*1,52 1013 ; T = 3*1,5 1013/2 = 4,5 1013/2 = 45 10 11/2 s.   E- d(P-b) = 2 1012 m. Vrai. dans le cas de P-b : T2/d3 =6 10-20 ; d3 = T2/ 6 10-20 = 16*3 1016/6 10-20 =8 1036 ; d = 2 1012 m.     Un astre A sphérique, de rayon RA= 5000 km, possède un satellite stationnaire S, c'est à dire restant constamment au dessus du même point de l'astre. On connaît la durée du jour sidéral de A, TA= 2 104 s et le champ de pesanteur à la surface de A, gA= 4 m/s². A- L'orbite de S appartient au plan équatorial de A. vrai B- S évolue à 5000 km d'altitude. vrai 3è loi de Kepler T²/r3 = 4p²/(gRA²) soit r3 = T²gRA² / (4p²)= 4 108*4*25 1012/40 =1021 soir r = 107 m = 104 km ; RA+h = 10000 km C- S évolue à la vitesse de 3200 m/s environ. vrai . v² =gRA²/r = 4*25 1012 / 107 = 107 ; v voisin 3200 m/s. D- Sa période est de 2 104 s. vrai Le satellite et l''astre ont la même période. E- Son vecteur accélération est nul. faux. accélération centripète de valeur : GMA/ (RA+h)²       Web www.chimix.com S1 et S2 sont deux satellites d'un astre A de masse M. Le satellite S1, de mase m1, a une trajectoire circulaire uniforme de rayon R autour de A. Le satellite S2 décrit une éllipse de demi grand axe a. On donne M=1031 kg, m2 = 1023 kg, m1 = 1024 kg, R= 1,5 108 km, a= 9R/4 et G= 20/3 10-11 SI.  a) La vitesse de S1 vaut 2/3 105 m/s. v² = GM/R= 20/3 10-11*1031/1,5 1011 = 2 1010/4,5= 20 1010/ 45 = 4/9 * 1010 ; v =2/3 105 m/s a)vrai b) La période de révolution de S1 autour de A est environ104p/8 heures. b)vrai T² / R3 = 4p²/(GM )( 3è loi de Kepler) T²= R3 4p²/(GM )=(1,5 1011)34p²*3 1011/20 * 10-31 = 1,53*6 p² 1012=1,52*9p² 1012. T= 1,5*3 p 106 s = 4,5 p 106/ 3600 heures = 4,5 p 104/ 36= p 104/ 8 heures c) La période de révolution de S2 autour de A est environ 104p/8 jours c) faux T²2= a3 4p²/(GM ) = (9R/4)3 4p²/(GM ) soit T²2= (9/4)3T² ; T2 = 3,37 T d) La vitesse de S2 a sa position la plus éloignée de A vaut racine carrée (GM/a) d) vrai e) L'aire balayée par le rayon vecteur AS1 pendant une durée donnée est égale à l'aire balayée par le rayon AS2 pendant la même durée. Le mouvement de chaque planète est tel que le segment de droite reliant le soleil ( astre central) et la planète balaie des aires égales pendant des durées égales.e) faux  A, B, C sont trois satellites de la Terre évoluant à des distances respectives D1, D2, D3 du centre de la Terre sur des orbites circulaires parcourues avec des périodes respectives T1, T2, T3. On note V1, V2, V3 les vitesses respectives des satellites. On donne D1= 3 D2 et T2 / T3 = 8/27. 1. D1/D3 vaut-il 4/3 ? vrai. d'où D1/D3 = 4/3. 2.T1/T3 vaut-il : 8 racine carrée (3) / 9 ? vrai. 3. V1/V3 vaut-il : racine carrée (3) / 2 ? vrai. 4. V1/V2 vaut-il : racine carrée (3) / 3 ? vrai. 5. Les trois satellites ont-ils une accélération tangente à leur trajectoire ? faux. Les satellites ne sont soumis qu'à la force de centripète exercée par la Terre. D'après la seconde loi de Newton, l'acélération est centripète, dirigée vers le centre de la Terre.

retour -menu