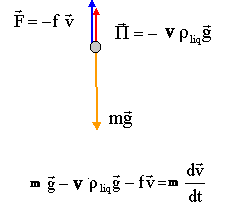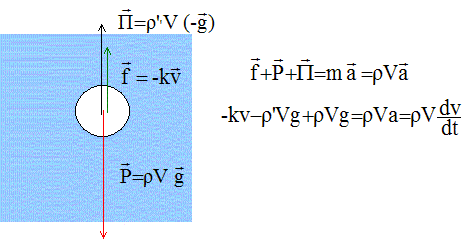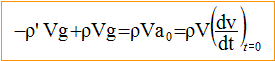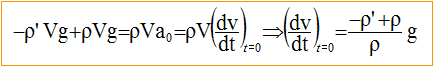Concours Esiee : 4 années de QCM réflexion, réfraction de la lumière.

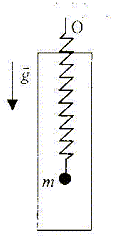
La masse m est attachée à l'extrémité d'un ressort sans masse. L'autre extrémité est fixée en O à un support immobile. On plonge la masse dans un fluide de masse volumique constante. A l'instant t=0 on lâche m sans vitesse initiale d'une position telle que m acquiert un mouvement pseudo-périodique en restant constamment dans le fluide. La bille est soumise à son poids, à la force de rappel du resort, à la poussée d'Archimède et à une force de frottement fluide du type -fv où f est une constante et v le vecteur vitesse à l'instant t. A- La vitesse de la bille tend vers une valeur limite non nulle. Faux. La bille va finir par s'immobiliser à la position d'équilibre. B- La force de rappel et la poussée d'Archimède sont toujours de sens opposé. Faux. C- La force de rappel et la force de frottement sont toujours de sens opposé. Faux.   D- Les vecteurs accélération et vitesse sont toujours de même sens. Faux.   E- La poussée d'Archimède varie au cours du temps. Faux. poussée = volume immergé * masse volumique du liquide * accélération de la pesanteur   A l'instant t=0 on lâche à partir de O et sans vitesse initiale une bille de masse m, de petites dimensions, pleine ( masse volumique r) dans un fluide de masse volumique rliq. Outre son poids et la poussée d'Archimède P la bille est soumise à une force de frottement fluide de valeur kv , où k est une constante, v la vitesse ( cette force colinéaire à la vitesse est de sens contraire à la vitesse ). Le récipient est suffisamment grand. m=20 g ; k= 20 SI ; rliq/r =0,4. A- L'équation différentielle vérifiée par la vitesse est dv/dt + kv/m =g (r-rliq)/r. vrai La bille est soumise à son poids, verticale vers le bas, valeur mg, à la poussée d'Archimède, verticale vers le haut, valeur rliq Vg à la force de frottement fluide, colinéaire à la vitesse, de sens contraire, valeur f= kv. V : volume du solide de masse m : m = r V suivant un axe vertical, orienté vers le bas, la seconde loi de Newton s'écrit : mg-Vrliq g - kv = mdv/dt ; r V g-rliqVg -kv = mdv/dt = r Vdv/dt ; dv/dt +kv/m = g( r-rliq) /r. B- La vitesse de m tend vers la valeur 0,06 m/s. faux vitesse limite r V g-rliqVg -kvlim =0 ; r V g-rliqVg =kvlim ; vlim = gV(( r-rliq))/k ; avec V= m/r ; vlim = mg( r-rliq)/(kr) ; vlim = mg( 1-rliq/r)/k = 0,02*10*0,6/20 = 0,006 m/s. C- La bille constitue un système conservatif. faux La force de frottement fluide est non conservative D- k s'exprime en kg s-1. vrai. kv s'exprime en newton (N) soit kg m s-2 ; v s'exprime en m s-1 ; k= force / vitesse s'exprime en kg s-1 E- P= 0,08 N vrai. Poussée d'Archimède = rliqVg = rliqm/r g = 0,4*0,02*10 = 0,08 N.       Web www.chimix.com A l'instant t=0, on lâche sans vitesse initiale, une bille pleine sphérique de masse volumique r, dans un fluide de masse volumique r'. Outre son poids et la poussée d'Archimède, la bille est soumise à une force de frottement fluide, colinéaire à la vitesse et de sens contraire, de valeur kv ( k est une constante). La taille du récipient est supposée très grande.   La vitesse tend-elle vers une valeur limite proportionnelle à k ? faux. Quand la vitesse limite est atteinte, les forces se neutralisent. -kvlim -r' Vg + r Vg=0 ; vlim = Vg(r-r')/ k.  L'accélération initiale de la bille est-elle nulle ? faux. A t=0, la vitesse est nulle : la force de frottement fluide est donc nulle. si r est différent de r ' l'accélération initiale n'est pas nulle.  Au bout d'un certain temps le mouvement devient-il uniformément accéléré ? faux. Au bout d'un certain temps, les forces se neutralisent ; d'après le principe d'inertie, la bille est animée d'un mouvement rectiligne uniforme. A t=0, l'accélération vaut-elle : ( r - r') g / r ? vrai. L'accélération de la bille à t=0 dépend-elle de k ? non. L'accélération initiale ne dépend pas de k.    A l'instant t=0, on lâche sans vitesse initiale une bille pleine sphérique, de rayon R et de masse volumique r, dans un fluide de masse volumique r '. Outre son poids et la poussée d'Archimède, la bille est soumise à une force de frottement fluide dt type -kv où k est une constante et v le vecteur vitesse à l'instant t. k dépend de la viscosité du fluide selon k= 20hR. La taille du récipient est suffisante pour obtenir l'évolution de la vitesse v pendant 3 s. Cette vitesse est représentée ci dessous par la courbe rouge dite de référence. On reprend la même expérience avec des billes de rayon 2R et un fluide de même masse volumique mais de viscosité 2h. L'expérience (x,y) correspond à la chute d'une bille de rayon x dans un fluide de viscosité y. a) La courbe a correspond à l'expérience (R ; 2h) La bille est soumise à son poids, verticale, vers le bas, valeur mg = r Vg = r 4/3 p R3 g - à la poussée d'Archimède verticale, vers le haut, valeur r' Vg=r' 4/3 p R3 g - à la force de frottement fluide, verticale, vers le haut, valeur 20hRv Lorsque la vitesse limite est atteinte la valeur du poids est égale à la somme des valeurs de la poussée d'Archimède et de la force de frottement mg=r g V = r ' g V + 20hRvlim avec V= 4/3 p R3. vlim = 4/3 p R2g(r -r ')/ (20h) La vitesse limite est proportionnelle au carré du rayon et inversement proportionnelle à la viscosité. 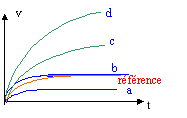R étant constant, si la viscosité double, la vitesse limite est divisée par 2.a) vrai b) La courbe b correspond à l'expérience (2R ; h) faux A viscosité constante, si le rayon double , la vitesse limite quadruple ( courbe d) c) La courbe c correspond à l'expérience (2R ; 2h) c) vrai La viscosité double ( vlim divisée par deux) mais le rayon double ( vlim multipliée par 4) : la vitesse limite double. d) La courbe d correspond à l'expérience (R ; 2h) faux e) La courbe de référence correspond aussi à l'expérience (2R ; 2h) faux

retour -menu