Concours Esiee : 4 années de QCM chute libre verticale, projectile.

On lance d'une altitude h une masse m supposée ponctuelle avec une vitesse initiale v0 verticale vers le haut. On néglige tout frottement. L'accélération de pesanteur est prise égale à 10 m/s². Entre l'instant du lancer et l'arrivée au sol, 2 s s'écoulent. h = 1,8 m ; m = 200 g ; v0 = 6 m/s. A- L'altitude maximale atteinte est 3,6 m. Vrai. On choisit un axe vertical orienté vers le haut dont l'origine est prise au sol. v (t) = -gt + v0 ; y(t) = -½gt2+v0t+h. v(t) = -10 t +6 ; y(t) = -5t2+6t+1,8. A l'altitude maximale la vitesse est nulle : 0 = -10 t + 6 soit t = 0,6 s. repport dans y(t) : ymax = -5*0,62 + 6*0,6+1,8 = 3,6 m. B- m met 0,6 s pour atteindre l'altitude maximale. Vrai. C- m repasse par sa position initiale 1,2 s après son lancement. Vrai. y= h conduit à : 1,8 = -5t2+6t +1,8 ; -5t2+6t =0 soit t = 0 et t = 1,2 s. D- m atteint le sol 1,8 s après son lancement. Faux. 0 = -5t2+6t+1,8. la résolution donne t = 1,45 s.   E- m atteint le sol avec une vitesse de 12 m/s. Faux. v = -10 t +6 = -10 *1,45+6 = -8,5 m/s. Le signe moins signifie que le vecteur vitesse est en sens contraire de l'axe.   On lâche d'une altitude h une masse m=200 g supposée ponctuelle avec une vitesse initiale v0, orienté vers le bas, de valeur 2 m/s. On néglige tout frottement. g= 10 m/s². Le temps de chute de m est de 2 s. A- h=20 m. faux. Chute libre avec vitesse initiale verticale. Suivant un axe vertical orienté vers le bas, dont l'origine est l'altitude h : h=½gt²+v0t = 5t²+2t ; h = 5*2²+2*2 = 24 m. B- Au bout d'une seconde "m" a parcouru ½h. faux h=½gt²+v0t = 5t²+2t ; h = 5*1²+2*1 = 7 m au bout d'une seconde de chute. C- La vitesse d'arrivée au sol est 22 m/s. vrai v = gt+v0 = 10 t + 2 = 10*2+2 = 22 m/s au sol. D - A l'altitude ½h la vitesse vaut 12 m/s. faux v² -v²0 = 2g(½h) ; v² =v²0+ 2g(½h) =2² + 10*24 = 244 ; v= 15,6 m/s. E- m atteint la vitesse de 12 m/s au bout d'une seconde. vrai v = gt+v0 = 10 t + 2 = 10*1+2 = 12 m/s à t=1 s.     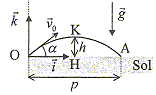Web www.chimix.com 1ère expérience : On lance de O, avec une vitesse v0 faisant un angle a avec l'horizontale une bille supposée ponctuelle. On note h1 la hauteur maximale atteinte par le projectile et p1 = OA la portée. On néglige tout frottement. 2ème expérience :on effectue un lancer similaire avec la même bille en gardant le même angle a mais en doublant v0. a) la hauteur maximale vaut 4 h1. b) la portée vaut 4 p1. p1= v0² sin(2a)/g : si la vitesse initiale double et a= cte alors p1 quadruple a) vrai h1= ½v0² sin²a/g : si la vitesse initialedouble et a= cte alors h1 quadruple b) vrai 3ème expérience : on effectue un autre lancer avec la même bille en gardant la même vitesse v0 mais en doublant l'angle a. c) La hauteur maximale vaut 2 h1. d) la portée vaut p1/2. Si v0= cte et si a double : sin²a ne quadruple pas, et la hauteur maximale ne double pas c) faux Si v0= cte et si a double : sin(2a) n'est pas divisé par 2 d) faux e) La norme de la vitesse en A est indépendante de l'angle de lancement a. Appliquer le théorème de l'énergie cinétique entre O et A ( le poids ne travaille pas car les altitudes de O et A sont identiques) en conséquence ½m v²O= ½m v²A et e) vrai On lâche simultanément d'une altitude h = 16 m deux objets ponctuels : - L'un de masse M1 = 200 g sans vitesse. - L'autre de masse M2=100 g avec une vitesse initiale verticale vers le bas de valeur Vo= 2 m/s. g=10 m/s. 1. Le temps de chute du premier vaut-il 1,6 s ? faux Mouvement de chute libre, seul le poids travaille. On choisit un axe vertical, orienté vers le bas, l'origine est à l'altitude h= 16 m par rapport au sol. Premier objet : vitesse V1 = gt= 10 t ; distance parcourue D1 = ½gt² = 5 t² Second objet : V2 = 10t + 2 ; D2 = 5 t² + 2t Durée de la chute du premier : t²= 16/5 = 3,2 ; prendre la racine carrée : 1,79 s. 2. A l'instant t= 0,5 s, la vitesse du premier vaut-elle 5 m/s ? vrai A t = 0,5, la vitesse du premier est : V1 =10 t = 10*0,5 = 5 m/s.   3. A l'instant t= 0,5 s, la vitesse du second vaut-elle 7 m/s ? vrai A t = 0,5 s la vitesse du second vaut : V2 = 10*0,5 +2 = 7 m/s 4. La vitesse d'arrivée au sol du second vaut-elle 18 m/s ? vrai Durée de la chute du second : 16 = 5 t²+2t ; 5 t² + 2t-16 =0 ; D½ = 18 Résoudre l'équation du second degré : t =1,6 s vitesse : 10*1,6 +2 = 18 m/s. 5. La vitesse d'arrivée au sol du premier vaut-elle 16 m/s ? faux Durée du parcours : 1,79 s A t = 1,79 s, la vitesse du premier est : 1,79*10 = 17,9 m/s. Or il y a seulement chiffres significatis dans les données : donc V arrondie à 18 m/s.   On lance de O avec une vitesse initiale v0 inclinée d'un angle a avec l'axe horizontal, une bille de masse m supposée ponctuelle. h=HK est la hauteur maximale atteinte par le projectile et p=OA la portée. On néglige tout frottement. On note Ec(X) et Ep(X) respectivement l'énergie cinétique et l'énergie potentielle de pesanteur de m en X. m= 100 g ; h= 10 m ; p/h=4 ; g= 10 m/s². A- tan a=1 vrai flèche h = v²0 sin²a/(2g) ; portée p= v²0 sin(2a)/g ; p/h =4 / tana = 4 ( a =45°) B- v0 = 20 m/s vrai h = v²0 sin²a/(2g) ; v²0 = 2gh/sin²a = 200/sin²a ; v0 =1,414*10 / sin 45 = 20 m/s. C- Ec(K)=0 faux la composante horizontale de la vitesse n'est pas nulle en K mais vaut v0 cosa. D- Ec(A)= 20 J vrai La variation d'énergie cinétique est nulle entre O et A ( O et A sont dans le même plan horizontal, le poids ne travaille pas) ; l'énergie cinétique en A est égale à l'énergie cinétique en O soit ½mv²0 = 0,5*0,1*20² = 20 J E- Ep(A)-Ep(K)=10 J faux énergie potentielle en K : mgh = 0,1*10*10 = 10 J ; O est prise comme origine de l'énergie potentielle ; Ep(A)-Ep(K)= -10 J.

retour -menu