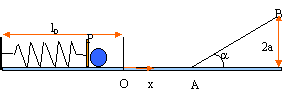Concours Esiee : 4 années de QCM Travail, énergie, théorème de l'énergie cinétique.

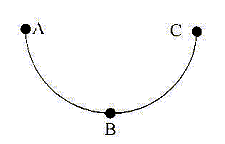
Les vecteurs sont écrits en gras et en bleu.  Un anneau de masse m glisse sans frottement sur un arc métallique ABC en forme de demi-cercle de rayon R= 10/p mètre. Outre le poids P et la réaction de l'arc sur l'anneau, deux forces F et F' d'intensité constantes de 100 N et 157 N respectivement agissent sur l'anneau. F reste tangente au cercle et dans le sens opposé au mouvement. F' agit selon la direction horizontale et de la gauche vers la droite. On note WXY(f) le travail d'une force f) sur le chemin menant de X à Y. On prend p = 3,14. A- WAB(F) = -500 J. Vrai. Puissance de F à la date t : P = F. v = -Fv ( vecteurs colinéaires de sens contraire) travail élémentaire sur le parcours noté ds = v dt : dW= -F v dt = -F ds Travail sur le parcours AB de longueur ½pR = 5 m : WAB(F) = -½pR F =-5*100 = -500 J. B- WAB(F) = WBC(F). Vrai. F et v vecteurs colinéaires de sens contraire ; F garde la même valeur ; le parcours a la même longueur. C- WAB(F') = 500 J. Vrai. Le travail d'une force constante ne dépend que des positions initiale et finale.( on choisit le parcours AO B avec O centre du cercle ) WAB(F') = WAO(F') + WOB(F') = AO * F' + 0 ( F' perpendiculaire à OB) WAB(F') = R F' = 10/p*157 =1570/3,14 = 500 J. D- WAB(F') = WBC(F'). Vrai. WBC(F') = WBO(F') + WOC(F') = 0+OC * F'= R F'. E- WAB(P) = WBC(P). Faux. Le travail d'une force constante ne dépend que des positions initiale et finale.( on choisit les parcours AO B et BO C avec O centre du cercle ) Travail moteur du poids en descente de O vers B ; travail résistant du poids en montée de B vers O.   Une masse m est attachée à l'extrémité d'un ressort sans masse de constante de raideur k et de longueur à vide L0. L'autre extrémité est fixée en O à un support immobile. On néglige tout frottement. On note x=OM la position de m sur l'axe Ox orienté vers le bas. On note g l'accélération de la pesanteur supposée constante. En O l'énergie potentielle de pesanteur est prise égale à 0. A- La position d'équilibre de m correspond au minimum d'énergie potentielle élastique. Faux. La position d'équilibre correspond à un minimum de l'énergie potentielle totale ( énergie potentielle élastique et énergie potentielle de pesanteur) Energie potentielle de pesanteur : -mgx ( origine en O) Energie potentielle élastique : : ½k(x-L0)2. Energie potentielle totale : Ep= ½k(x-L0)2-mgx. B- A la position d'équilibre de m, la somme des énergies potentielles est nulle. Faux. La position d'équilibre correspond à un minimum de l'énergie potentielle totale. dEp/dx= 0 donne k(xmini-L0)-mg soit xmini = mg/k + L0. Ep mini = ½k(xmini-L0)2-mgxmini = (mg)2/ (2k) -(mg)2/ k -mgL0 =-(mg)2/ (2k) -mgL0 = -mg(mg/(2k)+L0). C- La position d'équilibre de m correspond à xE= L0+mg/k. Vrai. A la position d'équilibre le poids de m compense la tension du ressort. mg = k(xE-L0) ; xE =mg/k + L0 La longueur du ressort est L= L0+mg/k. On lache m de A, xA > xE, sans vitesse initiale, m oscille alors en restant sur l'axe Ox entre les positions A et B. D- L'énergie cinétique de m est maximale lorsque l'énergie potentielle élastique est nulle. Faux. L'énergie mécanique se conserve ; l'énergie mécanique est la somme de l'énergie cinétique et de toutes les énergies potentielles. L'énergie cinétique est maximale lorsque l'énergie potentielle totale est minimale, c'est à dire à la position d'équilibre. Mais à la position d'équilibre l'énergie potentielle élastique vaut : ½k(xéq-L0)2. ½k(mg/k + L0-L0)2 = (mg)2/ (2k) E- Quand la masse m passe à la position d'équilibre, la vitesse est maximale. Vrai. A la position d'équilibre l'énergie potentielle totale étant minimale, l'énergie cinétique est maximale : en conséquence la vitesse est maximale.     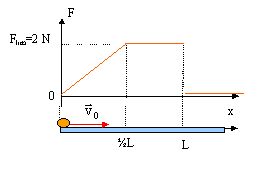Web www.chimix.com Un solide supposé ponctuel , de masse m= 100 g, est lancé en O avec une vitesse horizontale initiale v0= 6 m/s. Il est soumis à une force de frottement opposée au vecteur vitesse et dont l'intensité varie selon le graphe : a) Le solide s'arrête en x= L = 1 m. faux th de l'énergie cinétique entre 0 et L : ½mv²fin-½mv²0 = travail de la force de frottement ( - aire comprise entre la courbe rouge et l'axe Ox) travail de la force de frottement de x=0 à x=L : -½Flim ½L - Flim ½L = - 3/4 Flim L ½mv²fin-½mv²0 =0- 0,5*0,1*36 = -1,8 J -3/4 Flim L = -1,8 soit L =1,8*4/(3*2) ; L=1,2 m. b) La vitesse du solide en x= ½L vaut (26)½ / 2 m/s. faux . travail de la force de frottement de x=0 à x=0,5 L : - Flim*0,5L / 2 = -0,25 FlimL= -0,25*2*1,2=-0,6 J ½mv² - ½mv²0 = -0,6 ; v² = v²0 -0,6*2/0,1 =36-12 =24 ; v = 24½ m/s. c) La vitesse du solide en x= 0,25 L vaut (26)½ / 2 m/s. faux . travail de la force de frottement de x=0 à x=0,25L : -0,5 Flim*0,25L / 2 = -0,0625 FlimL= -0,0625*2*1,2 = -0,15 J ½mv² - ½mv²0 = -0,15 ; v² = v²0 -0,15*2/0,1 =36-3 =24 ; v = 33½ m/s. d) Le solide garde une vitesse constante entre x= ½L et x= L. faux . entre x= ½L et x= L, la bille n'est pas pseudo-isolée car la force de frottement n'est pas nulle e) Le travail de F entre x=0 et x= L vaut -3 FlimL/4. vrai A l'instant t=0, le ressort ( raideur k) est comprimé de a par rapport à sa longueur à vide l0. Une masse m, placée contre la plaque P, se trouve alors à l'abscisse -a. On libère le dispositif sans vitesse initiale. On néglige les frottements. La masse de la plaque est supposée très inférieure à m. On donne k/m= 10 et a= 1( dans le système MKS, mètre, kilogramme seconde) g= 10. 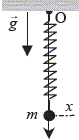Dans le cas où la masse m reste constamment solidaire de la plaque P, sa vitesse v à l'abscisse x est donnée par : v²= k(a²-x²)/m. vrai conservation de l'énergie mécanique: au départ ( t=0) : énergie potentielle élastique ½ka² à l'abscisse x ( solide au contact de P) : énergie potentielle élastique + énergie cinétique ½kx² + ½mv² ½kx² + ½mv² = ½ka² ; v²= k/m(a²-x²) Dans le cas où la masse m est simplement poussée par la plaque et libre de se séparer de celle-ci, la séparation intervient quand : b) x=0 ; c) x= +a La bille se sépare de la plaque lorsque le ressort passe par sa position d'équilibre O, alors x=0 b) vrai ; c) faux m rencontre un plan incliné d'un angle a= 30 ° par rapport à l'horizontale. Le point B se situe à une hauteur 2a par rapport à l'horizontale. d) La vitesse de m en A vaut 10 m/s. faux La vitesse de m en A est égale à la vitesse en O , car entre O et A le solide est pseudo-isolé ½ka² = ½mv²A soit v²A=k/m a² = 10 et vA = 10 ½. e) m atteint B. faux conservation de l'énergie mécanique entre A et B ( origine des altitudes A) EA= ½mv²A ; EB= ½mv²B +mg 2a ½mv²A = ½mv²B +mg 2a ; v²A = v²B +g 4a ; v²B= v²A- 4a g = 10 -40 un carré ne peut être négatif, donc B n'est pas atteint.   Une masse m= 100 g glisse de A en B sur un plan incliné d'un angle a sur l'horizontale. sin "a = 0,2. g= 10 m/s². x est la position du centre d'inertie de la masse. 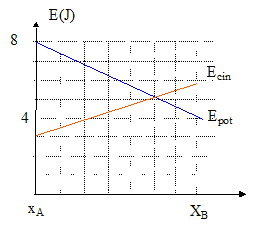Le mouvement de m est-il rectiligne uniforme ? faux. La trajectoire est une droite : le mouvement est rectiligne. d'après le graphe, l'énergie cinétique est une fonction croissante de l'abscisse x : l'énergie cinétique n'est pas constante et donc la valeur de la vitesse n'est pas constante : le mouvement n'est pas uniforme. m est-elle soumise à des frottements ? vrai. Energie mécanique = énergie potentielle + énergie cinétique En A : Em= 8+3 = 11 J ; en B : 6+4 = 10 J. L'énergie mécanique n'est pas constante : elle diminue, donc il existe des frottements. La différence d'altitude entre A et B vaut-elle 2 m ? faux. Origine des altitudes choisie au sol. Energie potentielle de pesanteur : Epot = mgh = 0,1*10 h = h En A : altitude = 8 m; en B : Dh= 4 m. Le rapport des vitesses de m en A et en B vaut 'il : Va/Vb = 0,5 ? Energie cinétique en A : ½mV²a= 3 Energie cinétique en B : ½mV²b = 6 V²a/V²b = ½ ; Va/Vb=0,50.5 =0,39. faux.

retour -menu