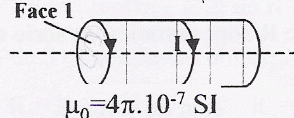|
Concours kiné Berck : 9 années de QCM Solénoïdes, force de Laplace |
||||||||
|
||||||||
|
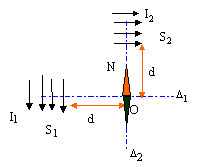
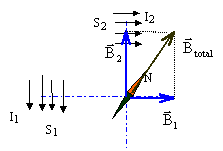
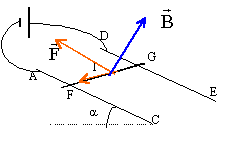
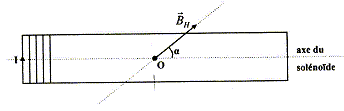
De quel angle en degré va pivoter la petite aiguille aimantée lorsque l'on établit simultanément I1 et I2 ? L'intensité du courant dans le solénoïde et le champ magnétique sont proportionnels.
tan a = B1/B2 = I1/I2 =1/1,5 = 0,67 ; a =33,7°.
B= m0nI
=4p 10-7
*450*18 10-3 = 1,02 10-5
T. tan a1 =
B/Bh = 1,02 10-5 / 2
10-5 = 0,51 et a1
=27°.
Un solénoïde de 500 spires, de longueur L= 60 cm est parcouru par un courant I= 5A.
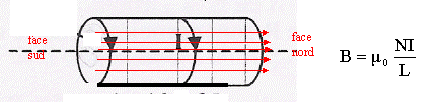
Parmi les affirmations suivantes, combien y-en-a-t-il d'exacte ? 1- A l'extérieur du solénoïde le spectre magnétique est très semblable à celui d'un aimant droit. 2- La face 1 du solénoïde est une face nord. 3- A l'intérieur du solénoïde, les lignes de champ sont parallèles. 4- A l'intérieur du solénoïde , la valeur du champ magnétique est inversement proportionnelle à la longueur L de la bobine. 5- A l'intérieur du solénoïde, la valeur du champ magnétique est environ 5 mT. Le champ magnétique est pratiquement nul à l'extérieur du solénoïde : le spectre magnétique du solénoïde ne peut pas être semblable à celui d'un aimant droit. La ressemblance est importante néanmoins, l'aimant droit ne possède que des plans de symétrie car c'est un parallélépipède rectangle tandis que le solénoïde possède un axe de révolution. Les lignes de champ résultante sont donc différentes en étant rigoureux. Si l'aimantation de l'aimant est uniforme et que l'aimant est cylindrique, l'équivalence (à l'extérieur !) est rigoureusement exacte.
B= 4*3,14 10-7*500*5/0,6 = 5,2 10-3 T voisin 5 mT 3 affirmations exactes : 3, 4 et 5.
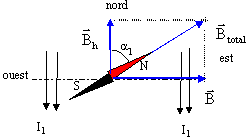
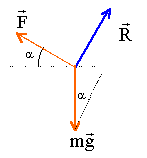
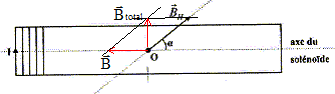
On place une aiguille aimantée en un point O à l'intérieur d'un solénoïde de longueur L=50 cm et comportant N=200 spires. En l'absence de courant, l'aiguille prend la direction de la composante horizontale BH du champ magnétique terrestre. Cette direction forme un angle de 45 ° avec l'axe du solénoïde. Lorsqu'on fait circuler un courant d'intensité I, on constate que l'aiguille tourne et forme un angle droit avec l'axe du solénoïde.
m 0=4p 10-7 S.I ; BH= 20 mT. Calculer l'intensité du courant (mA) qui circule dans le solénoïde. (28 ; 56 ; 122 ; 188 ; 250 ; aucune réponse exacte)
B= Btotal = BH sin 45 = 2 10-5 cos45 = 1,41 10-5 T de plus B= m 0N/L I soit I = BL/(m 0N)=1,41 10-5*0,5/(12,56 10-7*200)=2,81 10-2 A = 28 mA.
|
||||||||
|
|
||||||||
|
|