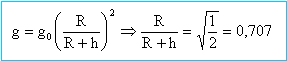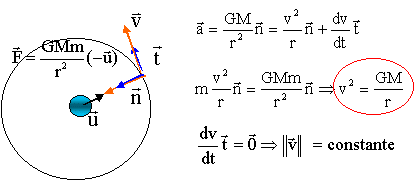Concours kiné Berck : 9 années de QCM satellite, 3è loi de Kepler, gravitation.

Un satellite décrit dans le repère géocentrique une orbite circulaire autour de la terre à une altitude h=6500 km. g=9,8 m/s² R=6370 km Déterminer l'accélération du satellite. Le satellite est soumis à l'accélération de la pesanteur à l'altitude h : a = g0 R² / (R+h)². R+h = 6370+6500 = 12870 km ; R/(R+h) =6370/12870= 0,495. a =9,8 *0,495² =2,4 m s-2. Ganymède est un satellite de Jupiter qui se déplace sur une trajectoire circulaire, à la distance R=1,07 106 km du centre de Jupiter. La période de révolution de Ganymède est T=171,7 heures. (G=6,67 10-11 SI). Quelle est la masse de Jupiter (kg). Ecrire la 3è loi de Kepler : T2/R3 = 4p2/(GM). M = 4p2R3/ (GT2) ; T= 171,7 h = 6,18 105 s ; R=1,07 109 m T2= 3,82 1011 s2 ; R3=1,225 1027 m3. M=4*3,142 *1,225 1027 /(6,67 10-11 *3,82 1011 )=1,9 1027 kg.   A quelle altitude h (en km) mesurée par rapport au sol, la valeur du champ gravitationnel terrestre est-elle égale à la moitié de sa valeur en surface. Rayon terrestre 6380 km R=0,707(R+h) ; R/0,707 -R = h ; h = 0,414 R = 0,414*6380 = 2644 km. La période de révolution d'un satellite en orbite circulaire autour de la terre est T= 5548 s. On place le satellite sur une orbite circulaire, la période du satellite augmente de 8%. G= 6,67 10-11 SI ; MT= 5,98 1024 kg ; RT= 6370 km. Déterminer l'altitude (en km) du satellite sur sa nouvelle orbite. Nouvelle période T1 = 1,08 T = 1,08*5548 = 5991,84 s. 3ème loi de Kepler : T²/r3 =4p²/(GM) 4p²/(GM) = 9,887 10-14.   T1²/r13 = 9,887 10-14 d'où r13 = T1² / 9,887 10-14 = 3,63 1020. r1 = 7134,3 km ; il suffit de retrancher le rayon terrestre (6370 km) pour obtenir l'altitude par rapport au sol : 764 km.     Web www.chimix.com Un satellite décrit autour de la terre une orbite circulaire de rayon r avec une période T. G = 6,67 10-11 SI ; rayon terrestre RT= 6380 km ; T= 1 h38 min ; masse de la terre MT= 5,98 1024 kg. Calculer la vitesse (km/h) du satellite sur son orbite. La période T est la durée pour pacourir une circonférence de rayon r à la vitesse v 2pr = vT 4p²r² = v²T² = GMT² / r T² = r3 4p²/ (GM) d'où r3 = T² GM / (4p²). T= 3600+38*60 = 5880 s r3 = 5880²* 6,67 10-11 * 5,98 1024/(4*3,14²)= 3,5 1020. r = racine cubique (3,5 1020) = 7,05 106 m vitesse 2 = GM/r = 6,67 10-11*5,98 1024 / 7,05 106 = 5,65 107 prendre la racine carrée : 7,5 103 m/s = 7,5 km/s 7,5 * 3600 = 2,7 104 km/h. Titan décrit une orbite circulaire de période T et de rayon r autour de la planète Saturne. On admettra que Titan et Saturne ont une répartition sphérique de masse. satellite période T(en j) rayon de l'orbite r ( en km) Titan 15,94 1,222 106 G= 6,67 10-11 SI ; densité moyenne de Saturne : d= 0,69. Déterminer le diamètre ( en km) de Saturne.( 5,8 104 ; 7,8 104 ; 9,2 104 ; 1,2 105 ; 1,9 105 ; aucune bonne réponse) 3ème loi de Kepler : T²/r3 = 4p²/(GMsaturne) donne Msaturne = 4p²r3 / (GT²) avec r = 1,222 109 m ; T= 15,94*24*3600 = 1,377 106 s. m = 690 kg m-3. Msaturne = 4*3,14²*(1,222 109)3 / (6,67 10-11*(1,377 106)2) =5,69 1026 kg. Volume de Saturne : Msaturne / d = 5,69 1026 / 690 = 8,25 1023 m3. 4/3pR3saturne= 8,25 1023 d'où R3saturne=1,97 1023 ; Rsaturne=5,81 107 m = 5,81 104 km ; diamètre = 1,2 105 km La planète Mars est assimilée à une sphère homogène de rayon R et à répartition de masse à symétrie sphérique. On a pu mesurer la force de gravitation exercée par mars sur une sonde spatiale de masse m à deux altitudes différentes : pour h1=4,82 104 km F1=40,2 N ; pour h2=7,76 104 km F2=16,3 N. Calculer la valeur du rayon ( en km) de la planète Mars. (2,9 103 ; 3,1 103 ; 3,3 103 ; 3,52,9 103 ; 3,7 103 ; aucune réponse exacte) F1= GMm/(R+h1)2 ; F2= GMm/(R+h2)2 ; F1/F2=[(R+h2) /(R+h1)]2 (R+h2) /(R+h1) =[F1/F2]½ ; [F1/F2]½ =[40,2/16,3 ]½ = 1,57 ; 1,57 (R+h1) =R+h2 ; R= (h2-1,57h1) /0,57 = (7,76 -1,57*4,82) 104/0,57 = 3,37 103 km.

retour -menu