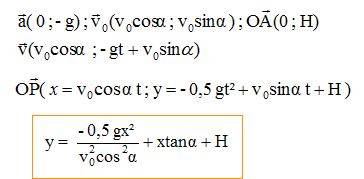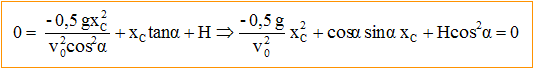|
Analyse détaillée d'exercices réalisés sous forme de QCM. Projectiles. |
||||||||
|
||||||||
|
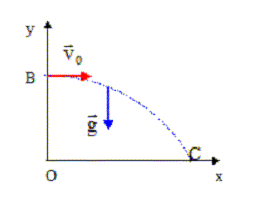
Texte : v0 = 57 km/h ; OB = H = 2,0 m ; on néglige les frottements. Analyse : Question relative à l'équation de la trajectoire. Exprimer v0 en m/s : v0 =57/3,6 = 15,8 m/s.
Question relative à la distance OC. Au point C, y=0 soit xC2 = 2v02H/g. xC2 =2*15,82*2/10 = 100 ; xC= 10 m. Question relative à la durée de la chute. xC = v0t ; t = xC / v0 = 10/15,8 =0,63 s. ou bien : yC=0 ; -0,5g t2+H=0 ; t2=2H/g ; t = (2H/g)½ = (2*2/10)½ =0,63 s.
La somme vectorielle des forces étant
verticale, seule la composante verticale de la
vitesse est modifiée: vC x = v0 et
vC y = -gt -10*0,63 = -6,3
m/s.
Lancer vertical sur la terre et sur la lune. Texte : vitesse initiale identique v0 ; glune = gterre /6. La balle de masse m = 0,1 kg est lancée verticalement vers le haut ; les frottements sont négligés. Analyse : Question relative à la hauteur maximale atteinte. L'altitude du point de départ est choisie comme origine des altitudes Au départ l'énergie mécanique de la balle est sous forme cinétique E=½mv02. Au point le plus haut, l'énergie mécanique est sous forme potentielle de pesanteur : mghmax. L'énergie mécanique reste constante : mghmax=½mv02 ; hmax=v02 /(2g). A v0 identique, l'altitude maximale est 6 fois
plus grande sur la lune que sur la
terre.
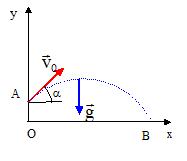
On choisit un axe vertical orienté vers le haut, ayant pour origine la position initiale de A ou B. Les frottements sont négligés. Analyse : Question relative aux équations horaires. A : vitesse initiale v0 ; accélération (-g) ; position initiale y0=0. à la date t : vA = -gt + v0 ; yA = -½gt2 +v0t. B : vitesse initiale -v0 ; accélération (-g) ; position initiale y0=0. à la date t : vB = -gt - v0 ; yB = -½gt2 -v0t. Question relative à H. H = |yA-yB| =2 v0t. Si v0 = 20 m/s et t=2 s alors H =80 m.
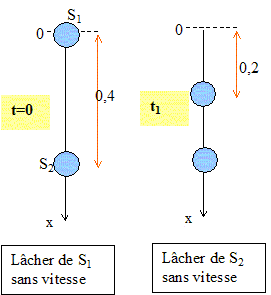
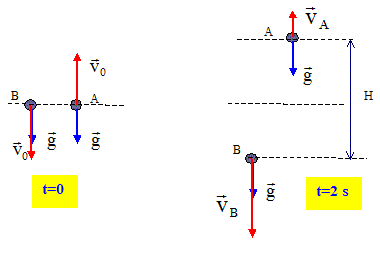
On néglige les frottements. g = 10 m/s2. Analyse : Question relative à la date t1. On choisit l'origine des dates au moment du lâcher de S1. La distance parcourue par S1 est : x1 = ½gt2 = 5 t2. 0,2 = 5 t12 soit t1 = (0,2/5)½ = 0,2 s. Question relative à la date de la rencontre. La distance parcourue par S2 est : x2 = ½g(t-0,2)2 +0,4= 5 (t-0,2)2 +0,4. x1 = x2 ; 5 t2=5 (t-0,2)2 +0,4 ; t2- (t-0,2)2 =0,4 /5 = 0,08. (2t-0,2)*0,2 =0,08 ; t = 0,3 s.
|
||||||||
|
|
||||||||
|
|
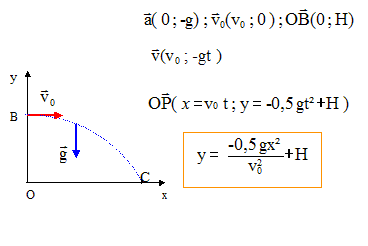
 On
néglige les frottements.
On
néglige les frottements.