Analyse détaillée d'exercices réalisés sous forme de QCM. Théorème de l'énergie cinétique ; puissance ; énergie mécanique

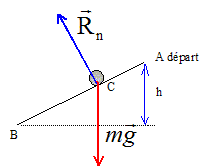
saut à skis. Texte : point de départ, haut du tremplin : la vitesse est nulle , l'altitude est prise égale à h =50 m. Bas du tremplin : l'altitude est choisie comme origine h0=0. Les frottements sont négligés ; g = 10 N/kg. Masse du skieur m = 80 kg. Analyse : Question relative aux travaux des forces . Le skieur est soumis à son poids et à l'action du plan. L'action du plan, perpendiculaire à la vitesse, ne travaille pas. Le travail du poids est moteur en descente et vaut : mgh = 80*10*50 = 4 104 J. Question relative à la vitesse en bas du tremplin. Ecrire le thèorème de l'énergie cinétique entre le point de départ et d'arrivée. Variation d'énergie cinétique ½mv2-0 ½mv2 = mgh soit v = [2gh]½ ; v = [2*10*50]½ = 1000½ = 31,6 m/s 31,6 *3,6 = 114 km/h.   Puissance d'une force. Texte : un cycliste roule à vitesse constante v = 43,2 km/h sur une route horizontale. Il est soumis à une force de frottement constante de valeur f = kv2, v étant la vitesse du cycliste et k une constante positive. La force de frottement est colinéaire à la vitesse mais de sens contraire. La puissance musculaire mis en oeuvre est égale à 690 W.   Analyse : Question relative l'unité de k. k = force / vitesse 2 ; force = masse fois accélération ; accélération = distance / temps2. d'où force : masse*distance / temps2.[force] =M L T-2. vitesse = distance / temps ; [v2] = L2 T-2. par suite : [k] =M L-1 ( kg m-1 ). Question relative à la valeur de k. Exprimer la vitesse en m/s : 43,2 / 3,6 = 12 m/s. La puissance mise en oeuvre par le cycliste compense à chaque instant la puissance perdue lors des frottements. La puissance d'une force est égale au produit scalaire du vecteur force par le vecteur vitesse ; dans ce cas les deux vecteurs sont colinéaires et de sens contraire ; ils sont en plus constants. Par suite la puisance des frottements vaut : -kv2*v = -kv3. kv3=690 ; k = 690/v3 ; k = 690/123 = 0,4 kg m-1.     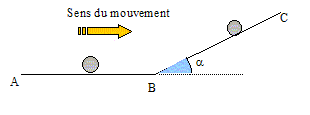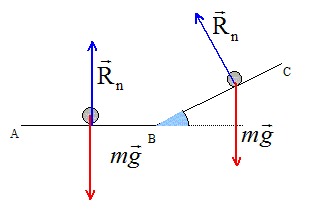Web www.chimix.com théorème de l'énergie cinétique. Texte : masse du solide m = 0,2 kg ; vitesse initiale en A : v0 = 6 m/s ; a = 16 ° ; g = 10 N/kg. Les frottements son négligés. Analyse : Question relative aux travaux des forces. L'action du sol Rn, perpendiculaire au plan, ne travaille pas. Le poids, perpendiculaire à la vitesse entre A et B, ne travaille pas entre ces deux points. Le travail du poids est résistant entre B et C et vaut : -mg BC sin a. Question relative à la vitesse en B. Entre A et B, les forces se neutralisent ; le solide est pseudo -isolé. D'après le principe d'inertie, le mouvement entre A et b est rectiligne et uniforme. La vitesse en B est identique à la vitesse en A. Question relative à la distance BC parcourue avant de redescendre. En C, il y a arrêt, avant la descente : la vitesse en C est nulle. variation de l'énergie cinétique entre A et C : 0-½mv02. th. de l'énergie cinétique : -½mv02 =-mgBC sin a ; BC = v02 / (2gsin a). BC = 62/(2*10 sin 16) = 6,5 m. Saut à l'élastique. Texte : masse du sauteur m = 50 kg ; vitesse initiale en haut du pont : v0 = 0 m/s ; g = 10 N/kg. caractéristiques de l'élastique : longeur à vide : L0 = 25 m ; constante de raideur k= 80 N/m. Les frottements son négligés. Analyse : Question relative aux forces appliquées au sauteur. Elastique non tendu : le sauteur n'est soumis qu'à son poids P= mg. Elastique tendu : le sauteur est soumis à son poids et à une force de rappel due à l'élastique de valeur F = k(L-L0) avec L : longueur de l'élastique Question relative à la hauteur minimale du pont. Question relative aux énergies. Le système est : { élastique + le sauteur }. L'origine de l'énergie potentielle est prise au niveau du sol. Energie mécanique initiale du sauteur = énergie potentielle de pesanteur = mgH , H hauteur du pont. Energie mécanique du sauteur au point le plus bas ( presque au sol) : L'énergie potentielle de pesanteur est nulle au sol ; le sauteur est à l'arrêt avant de remonter, son énergie cinétique est nulle. énergie potentielle élastique =½k(H-L0)2. Conservation de l'énergie mécanique : mgH = ½k(H-L0)2 : 2mg H/k = (H-L0)2 ; 12,5 H = H2-50H +625 ; H2-62,5 H +625 =0 ; D½ =37,5. La résolution donne H= 50 m.

retour -menu