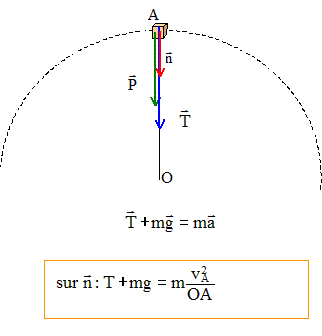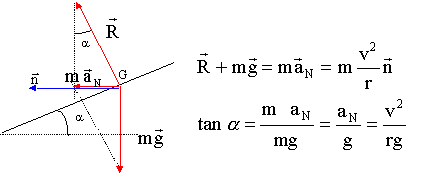Analyse détaillée d'exercices réalisés sous forme de QCM. Mouvement circulaire.

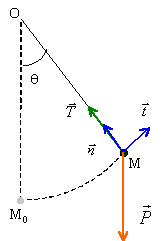
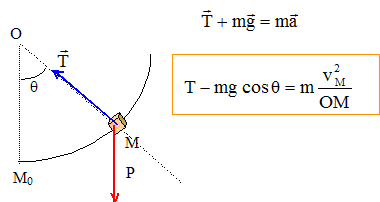
pendule simple. Texte :   La bille, de masse m, est lancée de la position d'équilibre stable M0 avec une vitesse v0 horizontale. Les frottements sont négligés. Analyse : Question relative à la tension T du fil. Question relative à la vitese initiale minimale permettant de faire un tour complet, le fil restant tendu.   La vitesse minimale de passage en A correspond à une tension nulle : vA2 = g OA = gL. Ecrire le théorème de l'énergie cinétique entre le point de départ et A : La tension perpendiculaire à la vitesse ne travaille pas. Travail résistant du poids en montée : -mg(2L) variation d'énergie cinétique : ½mvA2 -½mv02 ; ½mvA2 -½mv02 =-2mgL   v02 =vA2 +4gL = 5gL. A.N si L = 0,4 m alors v0 =[5*10*0,4]½ = 4,5 m/s.   Virage à vitesse constante. Texte : Un véhicule aborde un virage circulaire, de rayon R, à vitesse constante v0. Analyse : Question relative à l'accélération. L'accélération est centripète et vaut aN=v02/R A.N : v0 = 180 km/h ; R = 1 km. Exprimer la vitesse en m/s : 180/3,6 = 50 m/s ; R = 1000 m aN =502/1000 = 2,5 m/s2. Virage relevé. Texte : Un véhicule aborde un virage circulaire relevé, de rayon r, à vitesse constante v0. Question relative à l'angle a.       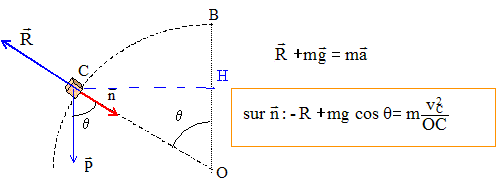Web www.chimix.com Glissement sur une sphère. Texte : un solide de petite dimension (S) de masse m = 50 g glisse sans vitesse initiale du sommet d'une sphère de rayon r = 60 cm. Les frottements sont négligés. Analyse : Question relative à l'action R du plan. R= m[g cos q -v2C/OC] Question relative à la vitesse à l'instant du décollage. Au moment du décollage, l'action du sol s'annule, R=0 soit : g cos q =v2C/OC ; v2C =g OCcos q. (1) Théorème de l'énergie cinétique entre B et C : L'action du sol, perpendiculaire à la vitesse, ne travaille pas. travail moteur du poids : mgBH = mgOB(1-cos q) ½mv2C-0 =mgOB(1-cos q) ; ½v2C-0 =gOB(1-cos q) ; v2C = 2gOB(1-cos q) (2) 1-cos q =v2C/(2gOB) =v2C/(2gOC) ; cos q =1-v2C/(2gOC) ; g OCcos q =gOC-½v2C. repport dans (1) : v2C = gOC-½v2C ; 1,5v2C = gOC ; v2C =gOC / 1,5. v2C = 10*0,6/1,5 =4 ; vC = 2 m/s. Question relative à l'angle q à l'instant du décollage. v2C =g OCcos q. (1) et v2C = 2gOB(1-cos q) (2) avec OB=OC=r g r cos q = 2g r (1-cos q) ; cos q = 2 (1-cos q) ; cos q =2/3.

retour -menu