|
|
|
réseau monophasé (25 kV, 50 Hz) On se propose d'étudier ici le fonctionnement simplifié d'une partie du TGV - Paris Sud Est. Nous étudierons en particulier l'alimentation des moteurs à courant continu : - soit à partir du réseau alternatif (25 kV, 50 Hz) ; - soit à partir du réseau continu 1 500 V. Les valeurs numériques présentes dans cet énoncé ont été modifiées de façon à simplifier les calculs, les ordres de grandeurs restent respectés. On dispose d'un réseau monophasé (25 kV, 50 Hz). On désire alimenter un pont mixte qui va permettre de commander un moteur à courant continu à excitation série. On intercale entre le réseau et le pont redresseur, un transformateur qui permet d'alimenter ce pont sous une tension alternative de valeur efficace 1 250 V. A - Etude du transformateur Ce transformateur a les caractéristiques suivantes : tension primaire nominale : U1n = 25 kV ; puissance apparente : 4 000 kVA On a réalisé deux essais qui ont permis d'obtenir les résultats suivants : *Essai à vide : tension primaire nominale tension secondaire à vide : U2o = 1,25 kV puissance absorbée au primaire : P1o = 2 kW *Essai en court circuit : tension primaire : U1cc = 1 kV courant secondaire : I2cc = 3 kA puissance absorbée au primaire : P1cc = 90 kW
B - Etude du pont mixte Dans cette partie, nous supposerons que : - la tension de sortie du transformateur est sinusoïdale de valeur efficace 1,2 kV ; - le courant d'intensité ic absorbé par le moteur (charge) est parfaitement lissé : ic = Ic ; - l'angle de retard d'amorçage q0 défini par rapport à la commutation naturelle est égal à 30 °. 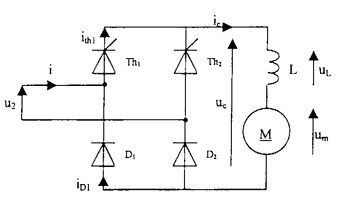
C - Etude du moteur à courant continu à excitation série Du point de vue électrique, la machine est équivalente au circuit suivant : 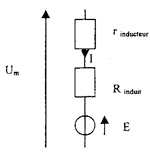 La machine est parfaitement compensée. Les grandeurs nominales sont les suivantes : Umn = 1 000 V ; In = 500 A; n = 3 000 tr.min-1. La vitesse de rotation du moteur est liée à la vitesse du train par la relation : v = N/10 (v en km.h-1 et N en tr.min-1). Pour un moteur de TGV, la résistance totale (Rt = R+r) est de l'ordre de 40 mW.
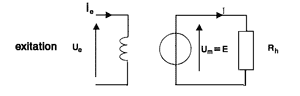 Un relevé de la caractéristique à vide à la fréquence de rotation de 2 000 tr.min-1 a donné les résultats suivants : ie = 200 A et E = 500 V. Lorsque le train roule à une vitesse de 100 km.h-1, calculer la fréquence de rotation, la force électromotrice, l'intensité du courant induit.
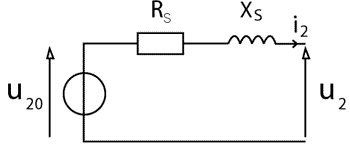
corrigé le transformateur : m = U20 / U1n =1250 / 25 000 = 0,05.
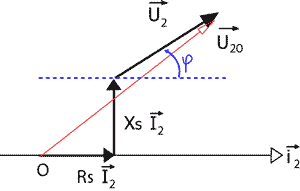
RS= P1cc / I²2cc = 90 000 / 3000² = 0,01 W. ZS= m U1cc / I2cc ; Z²S = R²S +X²S ; Recherche du déphasage par représentation de Fresnel.
DU2 = U20-U2 = RsI2cosj2+XsI2sinj2 = 0 tanj2 = -Rs/ Xs négatif, donc la charge doit être capacitive. Etude du pont mixte :
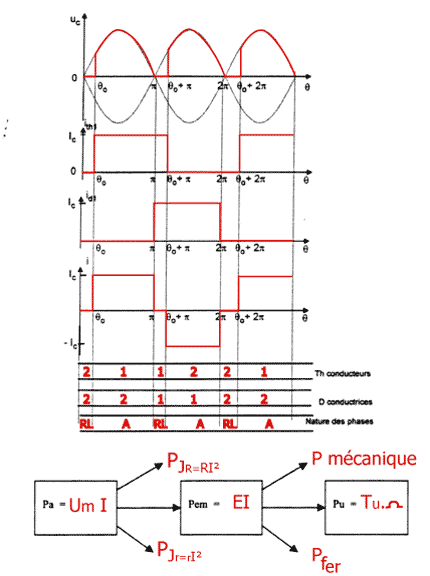
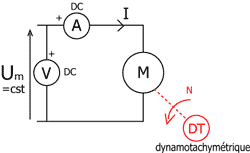
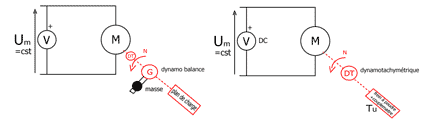
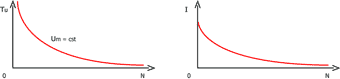
i = iTh1 - iD1 Pour mesurer sa valeur efficace, on utilise un ampèremètre numérique TRMS sur la position AC + DC ou un ampèremètre ferromagnétique. On mesure la valeur moyenne avec un voltmètre analogique magnétoélectrique sur la position DC ou avec un oscilloscope p(t) = uC(t) . iC(t) <p(t)> = P = <uC(t) . iC(t)> = <uC(t)> . IC P = U2 / p (1+cosq0)XC. Cette puissance est maximale pour q0 = 0 Cette puissance est minimale pour q0 = 180° Etude du moteur à courant continu à excitation série : Schéma de principe permettant de relever I = f(N) à Um = Cste.
Schéma de principe permettant de relever TU = f(N) à Um = Cste.
Procédure de mise en route : charger le moteur (appliquer un couple résistant) puis augmenter la tension Um. Procédure d'arrêt : diminuer la tension Um, car un moteur série s'emballe à vide sous tension nominale. On peut ensuite désaccoupler la charge. Umn = E + Rt In E = 1000-40 10-3 * 500 = 998 V. Pa = U I = 1 000 * 500 = 500 kW Pu = Pa - PJ - Pc = 500.103 - 10.103 - 10.103 = 480 kW à v = 100 km.h-1 N = 10 v = 10 x 100 = 1 000 tr/min Sachant que E = k . N alors E' = 250 V On applique la loi d'Ohm aux bornes de Rh I =Um / Rh = E'/ Rh = 250 / 0,5 = 500 A.
|
|
hacheur : On désire alimenter le moteur à courant continu sous une tension continue réglable entre 0 et 1 000 V. On intercale alors, entre le réseau et le moteur, un hacheur série. Etude du hacheur série Nous désirons étudier le montage suivant : 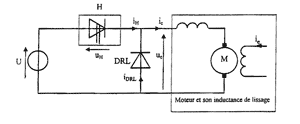
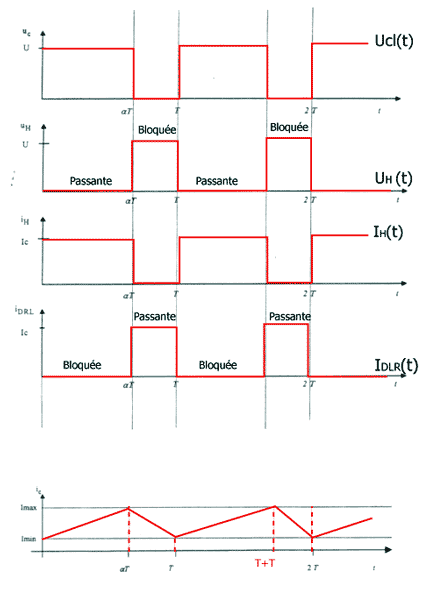
L'interrupteur H est fermé sur l'intervalle [0 ; aT] et ouvert sur l'intervalle [aT ; T]. Réseau U = 1 500 V
corrigé La diode de roue libre permet la continuité du courant ic dans la charge en dehors des phases d'alimentation.
<uc(t)>= aire de Uc / T = U aT / T =aU = 2/3 *1500 = 1000V. Loi des mailles (maille moteur) : uc(t) -uL(t) - um(t) = 0 uc(t) = uL(t) + um(t) On passe aux valeurs moyennes : <uc(t)> = <uL(t)> + <um(t)> Or <uL(t)> = 0 aux bornes d'une bobine Donc: <uc(t)> = <um(t)> Or on a um(t) = e(t) + R.ic(t) (fonctionnement moteur) D'où <um(t)> = <e(t)> + R.<ic(t)> = aU Au démarrage du moteur e(t) = 0 (moteur à l'arrêt) D'où : R.Ic = aU et a = R.Ic /U =0,03*500 / 1500 = 0,01. Même démonstration qu'au 3) On a : <iH(t)> = aIc . <iDRL(t)> = (1-a)Ic . On sait que ic(t) est constitué de portions de droite. Avec les points:Ic(0) = Imini ; Ic(aT) = Imaxi ; Ic(T) = Imini ; on peut tracer une période de ic(t) On a dans l'énoncé : ic(t) = [(U - E) / L] t + Ic min pour 0<t<aT et on sait que Ic (aT) = I c maxi ; d'où I c maxi =[(U - E) / L] aT + Ic min - L'énoncé nous donne : DIc = (I c maxi -Ic min )/2 en remplaçant on obtient : DIc =½[(U - E) / L] aT or T = 1 / f et E= aU (donné dans l'énoncé) donc DIc =½[(U - aU ) / L] a/ f DIc =½a(1-a)U/ (f L) On peut limiter l'ondulation du courant en augmentant la valeur de l'inductance le lissage L (on augmente alors son coût et son volume) ou celle de la fréquence de hachage f (on est limité par les possibilités de l'interrupteur H choisi et on augmente les pertes par commutation).
retour - menu |