Aurélie 06/02
induction électromagnétique

fiche cours

d'autres exercices

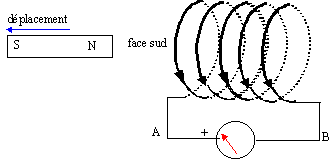
exercice 1 :

En position initiale, à proximité de la bobine, l'aimant crée un flux de valeur absolue | F1|= 75 mWb. On éloigne l'aimant en 0,5 s de telle sorte que en position finale, le flux à travers les spires de la bobine devient négligeable. Calculer :

  1. La valeur absolue de la fem induite moyenne.
  2. L'intensité moyenne du courant induit sachant que la résistance totale du circuit est R= 75 W.

corrigé
Pendant la durée du déplacement de l'aimant des phénomènes d'induction apparaissent dans la bobine :

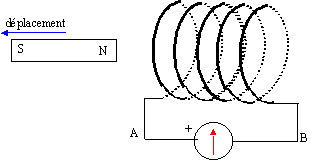
le circuit étant fermé on observe le passage d'un courant induit qui par ces effets électromagnétiques s'oppose à l'éloignement du pôle nord de l'aimant ; une face sud apparaît sur la bobine en face du pôle nord de l'aimant qui s'éloigne.

On en déduit alors le sens du courant induit i.

variation de flux : |DF|= 0,075 Wb

fem induite |e| = |DF| / D t = 0,075 / 0,5 = 0,15 V.

valeur moyenne de l'intensité = |e| / R = 0,15 / 75 = 2 10-3 A = 2 mA.

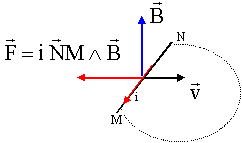
exercice 2 :

Un conducteur rectiligne MN de longueur L= 2 cm est plongé dans un champ magnétique uniforme vertical de module B= 50 mT. On déplace le conducteur horizontalement à la vitesse constante v = 2 m/s.

  1. Calculer la valeur absolue de la fem induite dans le conducteur.
  2. Préciser les polarités des extrémités M et N du conducteur.
 

corrigé
fem induite lors du déplacement du conducteur :

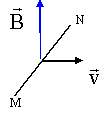
|e |= B MN v = 0,05 * 0,02 *2 = 2 10-3 V = 2 mV.

fermons le circuit, le courant induit qui prend naissance lors du déplacement de MN, par ces effets électromagnétiques s'oppose au déplacement de MN ; la force de Laplace induite est colinéaire à la vitesse mais de sens contraire.

On en déduit le sens de i et de la fem e( même sens que i). M borne positive et N borne négative.

 

Une bobine assimilable à un solénoïde, parcourue par un courant d'intensité i = 2,5 A, embrasse un flux propre F= 0,35 Wb. Calculer :

  1. L'inductance de la bobine.
  2. L'énergie emmagasinée.
  3. Le nombre de spires connaissant la longueur de la bobine l = 50 cm et le diamètre des spires d = 6,2 cm.
    m0 = 4 p 10-7.
corrigé
flux (Wb) = inductance (H) fois intensité (A)

F =L i d'où L= 0,35 / 2,5 =0,14 H.

énergie électromagnétique stockée : ½L i² = 0,5*0,14*2,5² =0,437 J.

nombre de spires N de la bobine :

champ magnétique crée par la bobine ;: B = m0 N / l i

flux propre : F = N B s = L i

remplacer B par son expression : m0 N² / l i s = L i

simplifier par l'intensité : m0 N² / l s = L soit N² = L l / (m0 s)

N = racine carrée (L l s /(m0 s) )

L= 0,14 H ; l = 0,5 m ; section s = p d²/4 = 3,14 * 0,062² / 4 = 3 10-3 m².

N = racine carrée ( 0,14*0,5 / (4 p 10-7*3 10-3)) = 4310 spires.

retour - menu