Aurélie 06/02
condensateurs

fiche cours

d'autres exercices

exercice 1 :

  1. Les caractéristiques d'un condensateur sont les suivantes : C= 0,12 mF, épaisseur du diélectrique e = 0,2 mm ; permittivité relative de l'isolant : e r= 5 ; tension de service : Us = 100 V. e 0= 8,84 10-12 F/m. Calculer :
    - La surface des armatures.
    - La charge du condensateur soumis à la tension de service.
    - L'énergie emmagasinée dans ces conditions.
  2. Le condensateur étant chargé, on l'isole, puis on l'associe en parallèle à un condensateur de capacité C1= 0,15 mF initialement déchargé. Calculer :
    - La charge totale de l'ensemble formé par les deux condensateurs.
    - La tension commune aux deux condensateurs en régime permanent.
    - L'énergie emmagasinée par le montage.
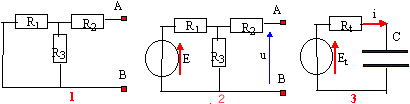
corrigé
C = e 0e r S / e soit S = C e / (e 0e r S)

S = 0,12 10-6 * 0,2 10-3 / (8,84 10-12 *5) = 0,543 m².

charge q = CUs = 0,12 10-6 *100 = 0,12 10-4 C = 12 mC.

énergie stockée : E = ½ CUs² = 0,5 *0,12 10-6 *100² = 0,6 10-3 J = 0,6 mJ.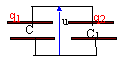

conservation de la charge q = q1 + q2= 12 10-6 (1)

exprimons la tension u de deux manières différentes : u = q1 / C = q2/C1.

soit q1 C1= q2C ; 0,15 10-6 q1= 0,12 10-6 q2 ou encore q1=0,8 q2 .

repport dans (1) : 0,8 q2 + q2= 12 10-6

q2 = 6,66 10-6 C et q1 = 5,33 10-6 C

tension u = 5,33 10-6 /0,12 10-6 =5,33 /0,12 = 44,4 V.

énergie stockée : E = ½ C u² + ½ C1 u² = ½(C+C1) u²

E = 0,5 ( 0,12 10-6 + 0,15 10-6 ) 44,4² = 2,66 10-4 J = 0,266 mJ.

Une partie de l'énergie initiale a été perdue ( effet joule, rayonnement électromagnétique lors de l'association)

exercice 2 :

Le condensateur est initialement déchargé.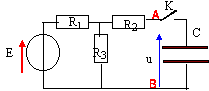

E=15 V ; R1 = 50 kW ; R2=R3 = 100kW ; C= 10 mF.

  1. Déterminer les élements Eth, rth,et Icc des modèles de Thévenin et de Norton équivalent du dipôle actif linéaire situé à gauche des bornes A et B, l'interrupteur K étant ouvert.
  2. Calculer l'intensité Ic du courant à la fermeture de K.
    - L'énergie du condensateur une fois sa charge terminée.
    - La durée approximative nécessaire pour que la charge du condensateur soit complète.
 

corrigé

le schéma (1) permet de calculer la résistance équivalente rt :

R1 et R3 en dérivation équivalentes à R = R1R3 / (R1+R3) = 33,3 kW.

R et R2 en série équivalentes à rt = R+R2 = 133,3 W.

le schéma (2) permet de calculer la fem u = Et :

aucun courant ne traverse R2 ; soit i l'intensité à travers R1 et R3 :

i = E / (R1+R2) et u = R3 i = R3 E / (R1+R2) =100*15 / 150= 30 V.

d'où l'intensité Ic du modèle équivalent de Norton : Ic = Et / rt = 10 /133,3 103 = 0,075 mA.

le schéma (3) permet de calculer l'intensité i :

en début de charge ( fermeture de K) l'intensité vaut 0,075 mA.

énergie stockée en fin de charge : ½C Et² = 0,5 * 10 10-6 * 10² = 0,05 J.

La durée approximative de la charge est égale à cinq fois la constante de temps t = rtC

5t = 133,3 103 = 10 10-5 = 6,65 s.

retour - menu