mécanique un choix de ressorts (première terminale )
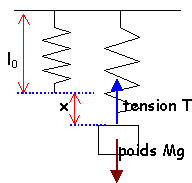
cours	position d'équilibre - énergie potentielle élastique
l0 : longueur à vide (m) x:déformation ou allongement (m) à l'équilibre , tension et poids sont opposées tension(N)= raideur (Nm-1)* allongement (m) poids(N) = masse (kg)* 9,8 (ms-2) énergie potentielle élastique 0,5 raideur* allongement ² = 0,5 kx²
exercice 1	courbe tension=f(allongement)
Compléter le tableau suivant: longueur du ressort à vide l0= 20 cm masse (g) 100 150 200 250 300 350 longueur (cm) 25 27,4 30 34,8 40 44,3 T:tension (N) x:allongement (m) Tracer le graphe T=f(x) en déduire la raideur. prendre g=10 ms-2.
..
corrigé
masse (g) 100 150 200 250 300 350 longueur (cm) 25 27,4 30 32,8 35 37,8 T(N)=masse (kg)*10 1 1,5 2 2,5 3 3,5 x(m)=longueur (m)-0,2 0,05 0,074 0,1 0,128 0,15 0,178
exercice 2	un tableau de mesures à interpréter compléter d'abord
masse accrochée(g) 100 150 200 250 300 longueur du ressort (cm) 20 24,9 30 35,6 40 tension (N) allongement (m) En déduire la raideur k et la longueur l0 du ressort. prendre g=10ms-2 .
..
corrigé
masse accrochée(kg) 0,1 0,15 0,2 0,25 0,3 longueur du ressort (cm) 0,2 0,249 0,3 0,356 0,4 tension (N)=masse(kg)*10 1 1,5 2 2,5 3 allongement (m) 0,1 0,149 0,2 0,256 0,2 raideur =T/ allongement 10 10,06 10 9,76 10 la longueur du ressort augmente de 10 cm à chaque fois que l'on accroche 100 g supplémentaires : l0=10 cm.
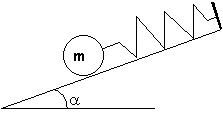
exercice 3	ressort en équilibre sur un plan incliné
l0=30 cm; k=20 Nm-1 ; m =100 g; a=15° Quelle est la longueur du ressort ?
.
corrigé
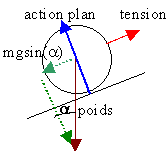
A l'équilibre la somme vectorielle des forces appliquées à la bille est nulle. T=mgsin(a) T=0,1*9,8*sin(15)= 0,253 N de plus T=k(l-l0) l=l0+ T/k = 0,3+0,253/20= 0,312 m
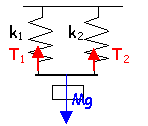
exercice 4	deux ressorts en parallèle
Quel ressort unique est équivalent à ce dispositif (longueur initiale et raideur) ? l0 :longueur à vide du ressort 1 l'0 :longueur à vide du ressort 2 l longueur commune de chaque ressort
..
corrigé
T1=k1(l-l0) ; T2=k2(l-l'0) ; A l'équilibre : Mg= k1(l-l0) + k2(l-l'0) Mg= ( k1+ k2) l -(k1l0 + k2l'0) Mg= ( k1+ k2)[ l - (k1l0 + k2l'0) /( k1+ k2)] raideur du ressort unique : k1+ k2 longueur à vide de ce ressort : (k1l0 + k2l'0) /( k1+ k2) si les deux ressorts sont identiques : 2 k et lo
		..
exercice 5	deux ressorts bout à bout
Quel ressort unique est équivalent à ce dispositif (longueur initiale et raideur) ? l0 :longueur à vide du ressort 1 l'0 :longueur à vide du ressort 2
.
corrigé
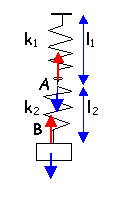
en A point immobile et sans masse les deux tensions sont égales T1=T2= k1(l1-l0) =k2(l2-l'0) en B : Mg= k2(l2-l'0) l'allongement du système est DL= ( l1+ l2) -(l0 + l'0) DL =( l2- l'0) + ( l1- l0) =( l2+ l'0) +k2 /k1(l2-l'0) DL =( l2- l'0)[ 1+k2 /k1] Mg= k2 / [ 1+k2 /k1] DL raideur du ressort unique : k2 / [ 1+k2 /k1]=k1k2 / ( k1+ k2) longueur à vide de ce ressort : l0 + l'0 si les deux ressorts sont identiques : 0,5 k et 2lo
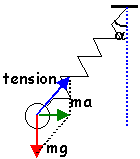
exercice 6	ressort suspendu dans un véhicule qui démarre
La vitesse du véhicule passe de 0 à 72 kmh-1 en 10 secondes. Un ressort est fixé au plafond du véhicule; à l'autre extrémité est fixé une masse m=100g. Quel est l'allongement du ressort lors de la phase de démarrage ? k=10Nm-1.
.
corrigé
variation de la vitesse du véhicule 72/3,6 = 20 ms-1. accélération du véhicule: 20 / 10 = 2 ms-2 . tan(a)=2/9,8 = 0,204 ; a= 11,53° tension = ma/ sin(a) = 0,1*2 / 0,2 = 1 N allongement = tension/raideur = 0,1 m
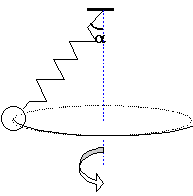
exercice 7	pendule conique
la vitesse de rotation est constante 120 tours par minute. masse de la bille accrochée au ressort m=200g la longueur du ressort est 50 cm raideur du ressort k=100 Nm-1. Quel est l'allongement du ressort ? Quel est l'angle a? Quelle est la vitesse de la bille ?
..
corrigé
vitesse angulaire : w=120/60*2p=12,56 rad s-1. Rayon du cercle : l sin(a) l'accélération est centripète aN=w²Rayon cercle =w² lsin(a) Tsin(a) = m w² lsin(a) T =m w² l =0,2*12,56²*0,5= 15,77 N T=kx ; allongement =15,77/100=0,157 m
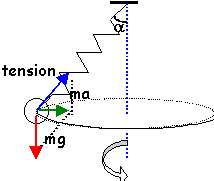
angle Tcos(a)=mg m w² l cos(a)=mg cos(a) = g / (w² l ) 9,8/ (12,56²*0,5)=0,124 ; a=82,8 °			vitesse v =w lsin(a) 12,56*0,5*0,991 =6,22 ms-1.
exercice 8	ressort et choc élastique
La masse m=50g est placée contre M=1kg quand le ressort est au repos. On comprime le ressort de a= 10 cm et on le libère. Il se détend et il y a choc élastique. k=400Nm-1. Calculer le vitesse V'1 de M et V'2 de m après le choc.
.
corrigé
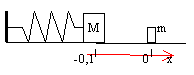
conservation de l'énergie du système M+ressort juste avant le choc (V1=vitesse de M). l'énergie potentielle élastique initiale est convertie en énergie cinétique 0,5 MV1² = 0,5 k a² ; V1²=k/M a²= 400/1*0,1²=4; V1=2 ms-1. conservation de l'énergie cinétique lors du choc 0,5 MV1² = 0,5MV'1² + 0,5 mV'2² 4 = V'1² + 0,05 V'2²(1) conservation du vecteur quantité de mouvement (projection sur Ox) après le choc les vitesses ont le sens de Ox MV1 =M V'1 + m V'2 2 = V'1 + 0,05 V'2 (2) la résolution du système de 2 équations donne: V'2 =3,81 ms-1 et V'1=1,81 ms-1.
..
exercice 9	propulsion à l'aide d'un ressort
La masse m=50g est placée contre M=1kg quand le ressort est comprimé de 10 cm et on le libère. Il se détend et la masse m est poussée progressivement k=400Nm-1. Calculer le vitesse de m après quelle ait quitté la masse M.
..
corrigé
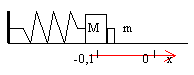
conservation de l'énergie du système M + m + ressort tant que les deux masses sont en contact (V1=vitesse de M). la variation d'énergie potentielle élastique est égale à l'énergie cinétique 0,5 k a² - 0,5 kx²= 0,5 (M+m)V1² lorsque x=0, m quitte M et le mouvement de m est rectiligne uinforme de vitesse V= a rac carrée( k/ (M+m)) =1,95 ms-1.
			retour - menu