réponses à vos questions mécanique (première terminale)
exercice 1	vecteur accélération
Un solide assimilable à un point matériel décrit une trajectoire horizontale. La valeur du vecteur vitesse du mobile est constante le long du tajet ABD puis elle augmente linéairement sur le trajet DE , enfin elle diminue linéairement entre E et F.
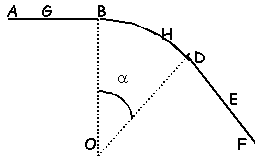
Sachant que la valeur du vecteur vitesse double entre les points D et E , trouver la valeur du vecteur accélération entre ces 2 points distants de 20m. On donne la vitesse en D :VD = 2 m.s-1 . Donner les caractéristiques (direction, sens, valeur) des vecteurs F , somme vectorielle des forces qui s'exercent sur le mobile , aux points H (qui appartient à BD) et G (qui appartient à AB. Faire les applications numériques correspondantes pour m=100g , rayon R=10 m,vitesse entre A et D = 2 m.s-1 . a=20°
..
corrigé
accélération sur le parcours DE VE² - VD² = 2 a*DE mouvement rectiligne uniformément accéléré a=(16-4)/(2*20)= 0,3 ms-2 L' accélération est nulle sur le parcours AB , le vecteur vitesse étant constant .mouvement rectiligne uniforme L' accélération est centripète sur le parcours BD, la norme de la vitesse est constante , mais la direction du vecteur vitesse change. mouvement circulaire uniforme a=V²/rayon=2²/10= 0,4 ms-2. norme de la somme des forces = m a =0,1*0,4= 0,04 N
exercice2	chute d'un pôt de fleurs...
Un pot de fleurs tombe sans vitesse initiale, de la fenètre d'un 5ème étage, d'une hauteur de 45m. Combien de temps dure la chute?A quelle vitesse arrive t-il au sol ? Au moment où le pot commence à tomber, un enfant,situé sur le trotoir et sous la fenètre, lance verticalement vers le haut une balle de tennis avec une vitesse initiale V0=25m/s. Ecrire la loi horaire du mouvement de la balle dans un repère orienté vers le bas et ayant pour origine le rebord de la fenètre. Déterminer la hauteur et la date de la rencontre. g=10ms-2.
..
corrigé
pot : chute libre verticale sans vitesse initiale z=5t² et v=10t 45=5 t² donc t=3 s et V=10*3= 30 ms-1. balle : chute libre verticale avec vitesse initiale z=5t²-25t+45 au moment de la rencontre : 5t² = 5t²-25t+45 d'où t =1,8 s et z=5*1,8²=16,2 m
exercice 3	vitesse angulaire de la terre
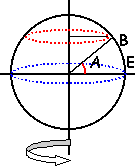
La terre tourne autour de son axe en un peu moins de 24 h par rapport au référenciel géocentrique. On appelle latitude d'un point B de la surface de la terre l'angle formé par les rayons OB et OE, où E est le point de l'équateur situé sur le même méridien que B. Calculer la vitesse d'un point situé à l'équateur par rapport au référenciel géocentrique.R=6400 km. Exprimer,en fonction de sa latitude A,la vitesse d'un point quelconque de la surface de la terre.
..
corrigé
vitesse angulaire de la terre w (rad s-1)=2p/ période (s) 2*3,14/(24*3600)=7,26 10-5 rad s-1. vitesse du point E : w *rayon OE (m)=7,26 10-5 *6,4 106 = 464,6 ms-1. vitesse du point B : w *R cos(A)
exercice 4	rendement d'un moteur thermique
Le moteur thermique d'un véhicule d'une entreprise de travaux publics a une puissance nominale de 30 kW. Il consomme 10 litres d'essence aux 100 Km lorsque la voiture roule à la vitesse constante de 120 km.h-1. A cette vitesse le moteur fonctionne à sa vitesse nominale. La combustion d'un litre d'essence libère une énergie de 33,5 MJ. Calculer l'énergie fournie par la combustion de l'essence consommée sur une distance de 200 km. Calculer le travail produit par le moteur pour parcourir cette distance à 120km/h. Calculer le rendement de ce moteur.
.
corrigé
énergie fournie par la combustion de 20 L d'essence 20*33,5 106= 6,7108 J=6,7108 /3600= 1,861 105 Wh= 186 kWh travail (J) produit par le moteur = puissance(watt)* durée (s) vitesse : 120/3,6 = 33,33 ms-1. durée du parcours : 200 *1000/33,33 = 6000 s travail =3 104*6000= 18 107J= 1,8 105 kJ =1,8 105/3600 = 50 kWh rendement: 100*50/ 186 = 26,88 %
exercice 5	gravitation et 3 ème loi de Kepler
Loi des périodes : les carrés des temps de révolution des planètes sont proportionnels aux cubes des grands axes des orbites. Dans le cas où l'orbite d'une planète peut être assimilée à un cercle de rayon R, en notant T la période de révolution de cette planète, traduire par une relation la loi des périodes. On considère les planètes Terre et Saturne dont les orbites seront assimilées à des cercles. La période T1 de Saturne est de 29,5 années .Sachant qu'une unité astronomique (u.a) est égale à la distance moyenne Terre-Soleil, déterminer en unités astronomiques le distance moyenne Saturne-Soleil. Gravitation universelle : FJ est la valeur de la force exercée par Jupiter sur le Soleil, FS la valeur de la force exercée par le Soleil sur Jupiter. FJ est elle supérieure, égale ou inférieure à FS ? Justifier. Une planète est un solide de masse à répartition sphérique. La valeur de la force de gravitation qu'elle exerce sur l'un des satellites serait elle modifiée si son diamètre était divisé par 2 et sa masse inchangée ? Justifier La masse de Saturne est 95 fois celle de la Terre ; la distance de Saturne au soleil est 905 fois la distance de la Terre au Soleil. Calculer le rapport de la valeur de la force de gravitation exercée par le soleil sur Saturne à celle exercée par le Soleil sur la Terre.
..
corrigé
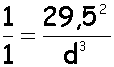d=9,54 u.a Les deux forces sont opposées (même valeur et de sens contraire) d'après le principe de l'action et de la réaction ( ou interactions mutuelles) . La force n'est pas changée car toutes les distances sont comptées à partir du centre de la planète, la masse étant ramenée au centre (corps à symétrie sphérique) Les forces de gravitation sont proportionnelles aux masses des planètes (donc 95 fois plus grande pour saturne) et inversement proportionnelles aux carrés des distances (donc 905² fois plus petite pour saturne) 95 / 905²=1,16 10-4
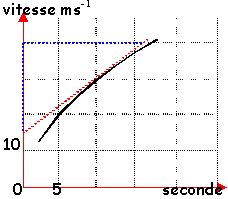
exercice 6	accélération : courbe vitesse en fonction du temps
Je dispose d'une courbe qui représente les variations de la vitesse d'une voiture en fonction du temps. On me donne la formule : a15=(v20-v10)/10 (a15 étant l'accélération de la voiture à l'instant t=15 secondes) On me demande maintenant de calculer l'accélération à l'instant 10 secondes. Je devrais faire : a10=(v15-v5)/10 je dispose d'un tableau: v km h-1 50 60 70 80 90 100 110 120 130 140 150 temps (s) 3,6 4,4 5,2 6,3 7,6 8,9 10,6 12,2 14,2 16,3 18,9
.
corrigé
v ms-1 13,55 16,66 19,44 22,2 25 27,7 30,55 33,3 36,1 38,9 41,7 temps (s) 3,6 4,4 5,2 6,3 7,6 8,9 10,6 12,2 14,2 16,3 18,9 coefficient directeur de la tangente à la courbe à t=10 s : 25 /16= 1,55 ms-2. en utilisant le tableau on trouve : (30,55-27,7) / (10,6-8,9)= 1,67 ms-2 ces deux résultats sont cohérents
exercice 7	accélération : un calcul classique
Une force constante F=80 daN agit sur un corps placé sur un plan horizontal. Au bout de 2 minutes, le corps acquiert une vitesse de 18 ms-1. Calculer: l'accélération du mouvement. la masse de ce corps.
.
corrigé
valeur de l'accélération(ms-2)=variation vitesse(ms-1) / durée de la variation (s) 18/(2*60) = 0,15 ms-2 la somme vectorielle des forces est égale au produit de la masse par le vecteur accélération du centre d'inertie G du solide. la somme des forces appliquée au solide est égale à F (le poids et l'action du support se neutralisent) 80 daN=800 N ; masse = 800/0,15 = 5333 N
exercice 8	Mercure et Jupiter vitesse angulaire
On admet que les mouvements de Mercure et de Jupiter , supposées ponctuelles , dans le référentiel héliocentrique sont circulaires et uniformes. Calculer leurs vitesses dans ce référentiel . Calculer leurs vitesses angulaires dans le même référentiel . En un an , quelles sont les angles A1 et A2 décrits par les deux planètes ? : Distance de Mercure au Soleil,D1=58.106 km : Distance de Jupiter au Soleil ,D2=778.106 km : Durée d'une révolution de Mercure autour du soleil ,T1=88j; : Durée d'une révolution de Jupiter autour du Soleil ,T2=4332j.
..
corrigé
Mercure Jupiter distance (m) 5,8 1010 7,78 1011 fréquence (hertz) =1/période (s) 1,315 10-7 2,69 10-9 vitesse angulaire (rads-1) = 2 p fréquence 8,26 10-7 1,678 10-8 vitesse (ms-1)=vitesse angulaire fois rayon(m) 47900 13058 angle décrit (rad) 365/période (j) *2p 26 0,53
exercice 9	vitesse limite d'une goutte de pluie
On admet que la résistance de l'air sur une bille sphérique de rayon R en chute libre peut se mettre sous la forme F=k R² v² avec v vitesse de la bille et k une constante qui dépend de la forme de l'objet. k=0,25 unité. Montrer que la bille atteint une vitesse limite Vm. Exprimer cette vitesse en fonction de g, R,k, et de la masse volumique de la bille. Calculer la vitesse limite d'une goutte de pluie de diamètre 2 mm. Calculer la vitesse du vent si vous voyez tomber la pluie à 60° par rapport à la verticale.
.
corrigé
La bille est soumise à 2 forces colinéaires et de sens contraire: le poids de la bille: mg=volume(m3)*masse volumique(kgm-3)*9,8 la résistance de l'air :F=k R² v² La vitesse augmente jusqu'à ce que les deux forces soient opposées : le mouvement devient alors rectiligne et uniforme 4/3 p R3 r g = kR²v² v²=4/(3k) p R rg v²=4/0,75*10-3*103*9,8=16,56 ; v=4,06 ms-1. 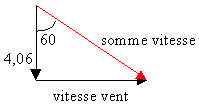vitesse du vent 4,06 tan(60) 7,03 ms-1
exercice 10	un bélier enfonce des pieux.
Un bélier de 500 kg, destiné à enfoncer les pieux, tombe d'une hauteur de 2,50 mètres. Calculer: sa vitesse au bas de la chute. son énergie cinétique. la résistance opposée par le sol à l'enfoncement du pieu(le pieu s'est enfoncé de 0,03 mètre après le premier coup).
..
corrigé
L'énergie mécanique se conserve. Au départ elle se trouve sous forme d'énergie potentielle de pesanteur mgh = 500*9,8*2,5 = 12250 J Avant le choc l'énergie est sous forme cinétique 0,5 mv²=250 v² vitesse = racine carrée (12250/250)= 7 ms-1. Lors du choc , l'énergie mise en jeu est égale au travail de la résistance du sol notée R R * 0,03 = 12250 ; R= 4 105 N.
retour - menu