radioactivité lycée
voir le Quiz : historique voir le match : ce qu'il faut retenir mots croisés
cours 1	quelques unités
Les noyaux instables se décomposent spontanément en émettant des particules et un rayonnement électromagnétique très pénétrant. L'ensemble de ces phénomènes est appelé radioactivité. unité de masse atomique : 1 u est égale au douzième de la masse de l'atome de carbone 12. 1 u =12 10-3/6 1023 = 1,66 10-27 kg électronvolt : 1 eV énergie acquise par un électron accéléré sous une tension de 1 V 1 eV=1,6 10-19 J E=mc² la masse est une forme de l'énergie. 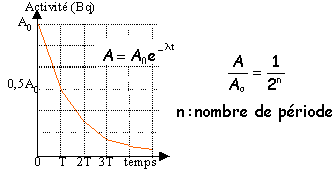j'exprime 1 u en MeV c-2 1,66 10 -27 * (3 108 )² =1,4 10-10 J 1,4 10-10*1,6 10-19 =931,5 MeV (M=106) 1 u=931,5 MeVc-2 loi de décroissance radioactive A : activité en Becquerel Bq nombre moyen de désintégrations par seconde. T : période radioactive ou demi vie durée au bout de laquelle l'activité est égale à la moitié de sa valeur initiale.
exercice 1	volume du noyau
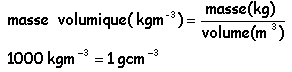
Calculer le rayon d'un noyau de l'élément cuivre (A=63 ) Calculer la masse volumique de ce noyau dont la masse est voisine de 63 u 1u=1,66 10-27 kg corrigé rayon du noyau R= 1,2 *63 exp (1/3) = 4,8 fm = 0,48 10-14 m masse du noyau : 63*1,66 10-27 = 1,05 10-25 kg volume du noyau (sphère): 4/3*3,14 (0,48 10-14 ) 3= 4,6 10-43 m3. 1,05 10-25 / 4,6 10-43 = 2,28 1017 kgm-3. trés grande comparée à celle du métal cuivre 8900 kgm-3.
exercice 2	énergie de liaison
c'est l'énergie libérée lors de la formation du noyau à partir des nucléons séparés au repos.  L'énergie de liaison par nucléon est voisine de 8 MeV pour la majorité des nucléides. Quelle est l'énergie de liaison par nucléon d'un noyau d'uranium 235. Z=92; masse du proton : 1,007 276 u; du neutron :1,008 665 u ; de l'électron : 0,000 549 u;masse du noyau d'uranium 235 :234,994 u corrigé  masse des constituants du noyau , séparés au repos 92 protons : 92*1,007 276 = 92,669 392 u 235-92= 143 neutrons 143* 1,008 665 = 144,239 095 u 92,669 392 + 144,239 095 = 236,908 487 u défaut de masse : 235 :234,994 - 236,908 487 = - 1,915 u 1,915 / 235 = 8,14 10-3 u par nucléon énergie de liaison par nucléon 8,14 10-3 *931,5 = 7,6 MeV par nucléon
exercice 3	réaction de fission
collision entre un neutron lent et un noyau d'uranium Enoncer les lois de conservation utilisées pour trouver Z et y. calculer l'énergie libérée par cette réaction . Calculer l'énergie libérée par kg d'uranium. Un réacteur nuclèaire a une puissance de 100 mégawatts. Quelle est la durée nécessaire pour consommer 1 kg d'uranium ? U: 235,043 915 u; Ba : 141,916 350 ; Kr : 89,819 720 u ; neutron : 1,008 665 u corrigé conservation de la charge : 92 + 0 = 36 + Z + y*0 d'où Z= 56 conservation du nombre de nucléons : 235 + 1 = 90 + 142 + y d'où y= 4 masse des réactifs : 235,043 915 + 1,008 665 = 236, 052 58 u masse des produits : 89,819 720 + 141,916 350 + 4,034 660 = 235,870 730 u défaut de masse : 235,870 730 - 236,052 58 = -0,28 185 u énergie libérée par noyau d'uranium 0,28 185 *931,5 = 262 MeV 262 106 * 1,6 10-19 = 4,19 10-11 J énergie libérée par mol d'uranium (235 g) 4,19 10-11 * 6,02 1023= 2,5 10 13 J ou 1,07 1014 J par kg puissance du réacteur = 10 8 watt ou 108 joules par seconde 1 kg d'uranium libère 1,07 1014 J 1,07 1014 / 108 = 1,07 106 s ou 12,2 jours.
exercice 4	réaction de fusion dans le soleil
Identifier x Quelle est l'énergie en MeV et J libérée par la formation d'un noyau d'hélium. La puissance rayonnée par le soleil est 3,9 1026 watts. Quelle est la perte de masse à chaque seconde ? La masse du soleil est 2 1030 kg. Son âge est 4,6 milliards d'années. Quelle masse a t'il perdu depuis qu'il rayonne ? masse H: 1,007 3 u ; He : 4,0015 u ; positon ou bien électron 0,55 10-3 u corrigé conservation de la charge : 4=2+2x d'où x=1 il s'agit d'un positon (électron positif) masse initiale : 4*1,007 3= 4,029 2 u masse finale des produits : 4,001 5 +2*0,55 10-3 = 4,002 65 u perte de masse : 4,002 65-4,029 2 = -0,026 6 u ou -0,026 6*1,66 10-27 = -4,41 10-29 kg énergie libérée : 0,026 6* 931,5 = 24,8 MeV 24,8 *1,6 10-19 = 4 10-12 J par réaction La puissance est l'énergie libérée chaque seconde soit : 3,9 1026 J pour une perte de 4,41 10-29 kg l'énergie libérée est 4 10-12 J diminution de masse du soleil à chaque seconde: 3,9 1026 / 4 10-12 *4,41 10-29 =4,3 106 tonnes expression de l'âge du soleil en seconde : 4,6 109*365*24*3600= 1,45 1017 s diminution de masse du soleil : 1,45 1017 * 4,3 106 = 6,2 1023 tonnes soit en pourcentage de la masse du soleil : 6,2 1026 / 2 1030 *100 = 0,03 %
exercice 5 datation par le carbone 14 Les neutrons cosmiques bombardent les noyaux d'azote de la haute atmosphère (1). Le carbone 14 se désintègre suivant (2). La proportion de carbone 14 est constante dans l'atmosphère et dans les organismes tant qu'ils sont vivants. A leur mort la quantité de carbone 14 décroît au cours du temps. Identifier Y et X. Sur un site préhistorique, des fragements d'os prélevés ont une activité de 113,75 désintégrations par heure et par gramme. Sur un fragement d'os d'un homme mort récemment, l'activité est 911,7 désintégrations par heure et par gramme. Quel est l'âge de l'os préhistorique ,(période du carbone 14 :T=5 500 ans) corrigé conservation du nombre de nucléons: 14 + 1 =14 + b d'où b=1 14 = d conservation de la charge : 7 = 6 + a d'où a=1 et X est l'élément hydrogène. 6 = -1 + c d'où c= 7 et Y est l'azote appliquer la loi de décroissance radioactive activité époque prèhistorique / activité actuelle 113,75 / 911,7 = 0,1247 0,1247 = 2 -n ou 1/ 0,1247 = 2 n n: nombre de périodes on trouve n=3 soit 3*5500 = 16 500 ans.
exercice 6		période, activité, constante radioactive.
1. Une certaine substance radioactive dont la demi-vie est de 10 s émet 2.107 particules alpha par seconde. Calculer la constante de désintégration de cet isotope. Calculer l'activité de cette substance Bq . Combien y a-t-il de noyaux radioactifs dans cette substance ? Combien en restera-t-il après 30 secondes ?   2 . On mesure en laboratoire l'activité spécifique de 235U. On trouve que 1 mg d'un échantillon d'Uranium 238 U émet 740 particules alpha/minute. Calculer la constante de désintégration de l'238U et sa période.   corrigé demi vie ou période = 10 s constante radioactive fois période = ln 2 =0 ,693 constante radioactive = 0,693 / 10 = 0,069 s-1. activité = nombre de désintégrations par seconde = 2 107 Bq nombre de noyaux radioactifs à la date t =0 : (instant de la mesure de l'activité) A = l N0 donne N0 = 2 107 /0,069=2,9 108 noyaux à t=0 . 30 seconde c'est trois périodes au bout d'une période : il reste ½ 2,9 108 noyaux ( la moitié a disparu) au bout de 2 périodes, 2,9 108 / 4 noyaux. pour 3 périodes , 2,9 108 / 8 = 3,6 107 noyaux. masse (g) / masse molaire (g/mol) quantité de matière (mol) 0,001 / masse molaire = 0,001 / 238 = 4,2 10-6 mol une mole d'atomes contient 6,02 1023 atomes 4,2 10-6 *6 ,02 1023 = 2,52 1018 noyaux d'uranium dans 1 mg au bout d'une période la moitié est désintégré soit 1,26 1018 noyaux 740 désintégrations en une minute, d'où la période : 1,7 1015 minutes ou 3,3 109 années constante radioactive fois période = 0,693 = ln 2 constante radioactive = 0,693 / 3,3 109 = 2,1 10-10 années-1.
exercice 7 : thalium plomb bismuth Tl Pb Bi Z=81 Z=82 Z=83 Il existe plusieurs isotopes du plomb, en particulier le plomb 210 et le plomb 214 tous deux radioactifs b-. Indiquer la composition de ces deux noyaux et écrire les deux équations des désintégrations radioactives. La période de désintégration ou demi-vie du plomb 214 est T1 = 27 min. - En déduire la valeur de la constante radioactive l1 en s-1. - Calculer l'activité d'un échantillon contenant 1 ng de plomb 214 sachant qu'il contient 2,8 1012 noyaux de plomb 214. On considère maintenant un échantillon contenant à t=0 autant de noayaux de plomb 210 que de noyaux de plomb 214. La période de désintégration ou demi-vie du plomb 210 est T2 = 22 ans. On note A1 l'activité du plomb 214 et A2 celle du plomb 210. t = A2/A1.Calculer t à t=0 et à t = 27 min. corrigé plomb 210 : 82 protons et 210-82 =128 neutrons plomb 214 : 82 protons et 214-82 =132 neutrons 21082Pb--> 21083Bi + -10e 21482Pb--> 21483Bi + -10e T1l1 = ln2 soit l1 = ln2 / (27*60) = 4,3 10-4 s-1. A = Nl1 = 2,8 1012 * 4,3 10-4 = 1,2 109 Bq. t = A2/A1= N2l2 / (N1l1 )=N2 T1 / (N1T2 ) à t = 0, N1 = N2 d'où t = T1 / T2 = 27 / (22*365*24*60) = 2,33 10-6. à t = 27 min, N1 est divisée par deux tandis que N2 reste pratiquement inchangée (22 min <<22 ans) d'où t double soit = 4,66 10-6.
DONNÉES :1 u (unité de masse atomique) = 1,6606 10-27 kg ; c = 3 108 m.s-1 ;NA = 6,022 1023 mol-1 ; e =1,6 10-19 C ; Masses de quelques particules :mproton = 1,6726 10-27 kg ; mneutron = 1,6749 10-27 kg Masses atomiques de quelques isotopes :23592U =235,044 u ; 14658Ce =145,910 u ;8534Se = 84,922 u Les réacteurs nucléaires. La France compte aujourd'hui 58 réacteurs nucléaires à eau sous pression (REP). La production d'énergie dans ces réacteurs repose sur la fission de l'uranium 235. En effet, lorsqu'un neutron heurte un noyau d'uranium 23592U, une des fissions possibles conduit à la formation d'un noyau de cérium 14658Ce et d'un noyau de sélénium 8534Se, ainsi qu'à un nombre a de neutrons. Écrire l'équation complète de cette réaction nucléaire ; en déduire la valeur de a. Justifier en exprimant les lois appliquées. - Calculer la variation de masse Dm qui accompagne la fission d'un noyau d'uranium 235. - Calculer, en joule et en MeV, l'énergie E libérée par cette réaction. Les centrales nucléaires françaises utilisant de l'uranium 235 fournissent au maximum une puissance électrique P = 1455 MW. La combustion d'un kilogramme de pétrole libère une énergie E = 45 106 J sous forme de chaleur. Le rendement de la transformation d'énergie thermique en énergie électrique est de 34,2 %. En déduire la masse de pétrole qui serait nécessaire pour produire pendant un an la même énergie électrique que les centrales nucléaires françaises. Étude des déchets et radioprotection La fission de l'uranium 235 produit, entre autres nucléides, le césium 137, émetteur radioactif g. Un employé de la centrale reste accidentellement durant une heure à proximité de la source de 1,0 g de césium 137. Durant cette exposition, il absorbe, uniformément sur l'ensemble du corps, 5 % des rayons g d'énergie 0,66 MeV émis par cette source. On suppose que l'activité de cette source est égale à 3,0 1012 Bq. Sachant que l'employé a une masse de 70 kg, calculer la dose absorbée en gray (ou J.kg-1). - La notion de dose n'est pas suffisante pour expliquer les relations " doses-effets ". C'est pourquoi on lui assortit un paramètre " qualité " du rayonnement traduisant la nature du rayonnement incident. Ainsi le produit de ce coefficient appelé EBR par la dose absorbée traduit une " dose équivalente " exprimée en sievert (Sv) ; la dose maximale annuelle autorisée est de 50 mSv. Calculer la dose absorbée reçue par l'employé de la centrale victime de l'accident sachant que l'EBR vaut dans ces conditions 0,06. Commenter ce resultat. corrigé 23592U + 01n = 14658Ce + 8534Se + a 01n conservation de la charge : 92 +0 = 58+34 +a*0 conservation du nombre de nucléons : 235 +1 = 146 +85 + a soit a = 5 Dm = |masse produits - masse des réactifs| D m = |145.910+84.922+4*1.0086-235.044|=0,1776 u multiplier par 1,66 10-27 = 2,94 10-28 kg E= D m c² = 2.94 10-28*9 1016 = 2,653 10-11 J diviser par 1,6 10-13 : 165,8 MeV. puissance (watt) * durée (seconde) = énergie (J) 1,455 109 3600*24*365 = 4,6 1016 J pour un kg de pétrole on produit : 4,5 10 7*0,342 = 1,54 107 J électrique masse de pétrole : 4,6 1016 / 1,54 10 7 = 3 10 9 kg. à chaque seconde 3 1012 noyaux de césium se désintègrent libérant une énergie de : 3 1012*0,66 = 1,98 1012 MeV soit 1,98 1012*1,6 10-13 = 0,32 J en une heure : 0,32*3600 = 1140 J énergie reçue : 1140 *0,05 = 57 J soit par kg : 57/70= 0,81 J/kg dose équivalente: 0,81 *0,06 = 4,9 10-2 Sv = 49 mSv à la limite de la dose annuelle autorisée.
retour - menu