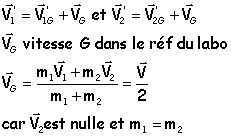_

chocs de 2 points matériels sup
cours 1	quantité de mouvement - impulsion
Soit un point matériel de masse m, soumis à des forces de résultante F; son mouvement est rapporté à un référentiel galileen vecteur quantité de mouvement = masse (kg) * vecteur vitesse (ms-1) vecteur impulsion d'une force pendant le temps t = vecteur force F(N) *t (s). si la durée est courte on parle de percussion; Au cours d'un choc, la quantité de mouvement totale du système des 2 corps qui se heurtent se conserve. choc parfaitement élastique l'énergie cinétique totale du système se conserve choc parfaitement mou l'énergie cinétique ne se conserve pas . 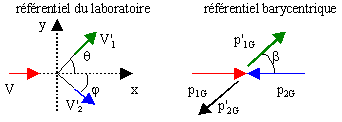A prés le choc les deux points ne forment plus qu'un seul point de masse m1+ m2 , de vecteur vitesse V étude dans le référentiel barycentrique référentiel d'origine G, barycentre des deux points, d'axes parallèles à ceux du référentiel avant le choc, le vecteur qté de mouvement total est nul après le choc, le vecteur qté de mouvement total est nul
exercice 1	choc élastique
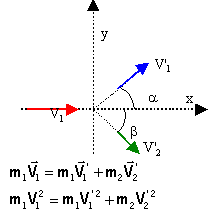
Un point matériel M1 de masse m1 est animé avant le choc d'une vitesse V1. Le point matériel M2 de masse m2 est au repos. Le choc est supposé élastique. Après le choc les vitesses de M1 et M2 sont V'1 et V'2 et font des angles a et b avec la direction de V1. Exprimer V'2 en fonction de V1, m1, m2 et b. corrigé projetons la relation vectorielle sur les axes m1V1 = m1V'1cosa + m2V'2cosb (1) 0 = m1V'1sina + m2V'2sinb (2) m1V'1cosa = - m2V'2cosb + m1V1 (3) m1V'1sina = - m2V'2sinb (4) élever (3) et (4) au carré puis ajouter (m1V'1)² = (m2V'2)² +( m1V1)²-2m1m2V1V'2cosb utiliser la consevation de l'énergie cinétique V'2 = 2m1V1cosb /(m1+m2)
exercice 2	choc mou
Un ressort vertical de raideur k est fixé à son extrémité inférieure. Il supporte un plateau de masse M à son extrémité supérieure. Un point matériel de masse m tombe d'une hauteur h (sans vitesse initiale). Le choc est parfaitement mou. L'énergie potentielle de pesanteur est considérée comme constante lors de la compression du ressort. Déterminer la déformation maximale du ressort corrigé vitesse de m juste avant le choc: lors de la chute diminution d'énergie potentielle de pesanteur + augmentation d'énergie cinétique = 0 -mgh + 0,5 mv²= 0 ......v²= 2gh. vitesse V de l'ensemble (M+m) juste après le choc (M+m)V =mv conservation du vecteur qté de mouvement L'énergie mécanique du système {ressort-plateau-projectile } se conserve. Soit a la déformation maximale du ressort énergie potentielle élastique finale 0,5 ka² énergie cinétique juste après le choc 0,5 (M+m)V² l'énergie potentielle de pesanteur varie peu si a est petit 0,5 ka² = 0,5 (M+m)V² a²= 2m²gh / (k(M+m))
exercice 3	choc partiellement élastique
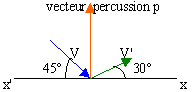
Un point matériel tombe sous une incidence de 45 ° sur une paroi lisse horizonale . Il rebondit en faisant un angle de 30° par rapport à l'horizontale. le choc est partiellement élastique.coefficient de restitution k : V'N=kVN vitesses normales à la paroi après et avant le choc. Calculer k et la vitesse après le choc. corrigé conservation du vecteur quantité de mouvement (projection sur x'x) V cos(45)=V'cos(30) V' =V rac carrée (2/3) projection sur la normale: VN=V sin(45)  ; V'N=V'sin(30)=0,5 V' ; k=V'N / VN= 0,5 V' / V sin(45) = 0,5 V rac carrée (2/3) / V sin(45) k= 1 /(rac. carrée (3))= 0,588
exercice 4	étude dans le référentiel barycentrique
Soient 2 particules M1 et M2 de même masse m. M2 immobile par rapport au référentiel du labo; M1 animé de la vitesse initiale V. Le choc est élastique. Exprimer V'1, V'2, q et j en fonction de V et b. corrigé Le choc est élastique, l'énergie cinétique se conserve: p²1G/2m +p²2G/2m =p'²1G/2m +p'²2G/2m de plus p1G= p2G et p'1G= p'2G conséquence p1G= p2G = p'1G= p'2G Les masses étant identiques :V1G= V2G =V'1G= V'2G composition des vitesses : V²'1= V²'1G+V²G+2V'1G*VGcos(b) et V'1G=V1G=V/2 conséquence : V²'1= 0,5V²(1+cos(b) V²'2= 0,5V²(1-cos(b) V²'1+V²'2= V² conservation de la qté de mouvement (réf du labo) mV=mV'1cos(q)+mV'2cos(j) projection axe des x 0=mV'1sin(q)-mV'2sin(j) projection axe des y V=V'1cos(q)+V'2cos(j) à élever au carré 0=V'1sin(q)-V'2sin(j) à élever au carré puis ajouter : V²=V²'1 + V²'2 + 2V'1V'2cos(q+j) identifier à (1) d'où : cos(q+j)=0 ..........q+j = p/2 soit sin(q)=cos(j) 0=V'1sin(q)-V'2sin(j) s'écrit V'1cos(j)=V'2sin(j) remplacer V'1 et V'2 par leurs valeurs sachant que tan²(j)+1 =1/cos²(j) cos²(j)=0,5(1-cos(b)
retour - menu