_

champ magnétique sup
cours 1	champ magnétique crée par une spire circulaire en un point de son axe
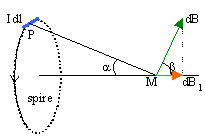
l'élément de courant Idl crée en M , le champ élémentaire dB, perpendiculaire à PM, de module : Idl et PM étant perpendiculaire sin(q)=1 Par raison de symétrie le champ résultant sera porté par l'axe horizontal. La composante utile sera dBcos(b) = dBsin(a) Pour tous les éléments Idl, l'angle a et PM sont les mêmes. L'intégration de dB sur toute la spire donne le module du champ résultant ( sin a = rayon r / PM )
cours 2	champ magnétique d'un solénoïde
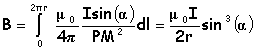
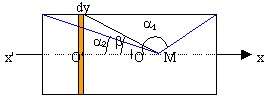
O est l'origine de l'axe. On pose O'M=y. La tranche de solénoïde de rayon R, d'épaisseur dy compte n1dy spires (n1 : nombre de spires par mètre). D'après l'exercice précédent, le champ dB crée par cette tranche est : dB = m0I/(2R) sin3(b) n1dy exprimons dy en fonction de db y= R cotan(b) dy=Rdb /sin²(b) d'où sin²(b)dy = Rdb dB = m0I/2 sin(b) n1db=m0I/2 n1d(-cos(b)) intégrer entre les angles a1 et a2. B=m0I/2 n1(cos(a2)-cos(a1)) solénoïde infiniment long a2=0 et a1=p B=m0 n1I
cours 3	champ magnétique crée par un fil infini
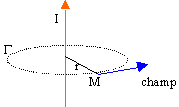
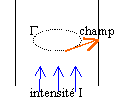
En tout point de G le champ magnétique a même module et est tangent à G. appliquer le th. d'Ampère sur le contour G, cercle de rayon r
cours 4	champ magnétique crée par un conducteur cylindrique
La densité de courant est j=I/(pR²), R rayon du câble. point intérieur au câble En tout point de G le champ magnétique a même module et est tangent à G. appliquer le th. d'Ampère sur le contour G, cercle de rayon r, l'intensité des courants enlacés par G étant I r²/R² B 2p r =m0 I r²/R² B =m0 I r / (2p R²) point extérieur au câble appliquer le th. d'Ampère sur le contour G, cercle de rayon r, l'intensité des courants enlacés par G étant I B 2p r =m0 I B =m0 I / (2p r) si r =R on peut constater que le champ magnétique donner par les deux expressions ci dessus a la même valeur. Continuité du champ magnétique lors du passage du conducteur au vide.
retour - menu