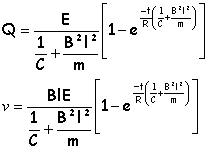_

physique : induction sup
cours 1	loi de Faraday - loi de Lenz
Un circuit fermé traversé par un flux magnétique F variable est le siège d'une force électromotrice d'induction e=-dF/dt Le courant induit s'oppose par ses effets à la variation de flux qui lui a donné naissance ( principe de modération). quantité d'électricité induite entre les instants t1 et t2 Q = (F1-F2)/R R résistance du circuit(W) Q en coulombs F en webers applications : courants de Foucault : courants qui prennent naissance dans un volume métallique qui est : soit mobile dans un champ magnétostatique (il y a freinage de la pièce mobile---> ralentisseur des camions) soit fixe dans un champ variable (si un aimant tourne devant un disque conducteur, celui ci est mis en mouvement dans le sens de rotation de l'aimant---> moteur asynchrone) effet calorifique ---> four à induction 2. générateurs électromagnétiques Le segment MM'=l, animé d'une vitesse v , est placé dans un champ magnétique uniforme B. Pendant le temps dt le segment balaye une surface d'aire dS=lvdt et le flux coupé est :dF=Blvdt d'où la force électromotrice induite e=-Blv Cette fem a un sens tel que le courant induit i s'oppose au déplacement de MM'. On a ainsi réalisé un générateur.
cours 2	courant induit dans une bobine tournante
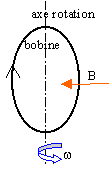
Une bobine plate circulaire, de rayon r comptant N spires tourne à vitesse constante w. Elle est placée dans un champ magnétique uniforme B. R étant la résistance totale du circuit calculer le courant induit. Si le champ magnétique n'est pas constant, le déterminer afin que le courant induit soit nul à tout instant. Considérer 2 cas : le champ à une direction constante et un module variable le champ à une direction variable et un module constant flux traversant la bobine à l'instant t: F = N B pr² cos(wt) fem induite : e= - dF/dt e = N B pr² w sin(wt) le courant induit est : i = e /R = N B pr² w/R sin(wt) La direction de B étant constante, l'expression du flux ne change pas F = N B pr² cos(wt) dériver par rapport au temps dF/dt= - N B pr² w sin(wt) + N pr² cos(wt) dB/dt le courant induit est nul si dF/dt=0 dB/B=w sin(wt) dt / cos(wt) = -d(cos(wt)) /cos(wt) intégrer : B=B0/cos(wt) Le module de B est constant , dF/dt sera nul si wt=constante la bobine et le champ doivent tourner à la même vitesse angulaire.
cours 3	rotation de 2 disques
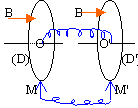
Deux disques identiques de rayon r sont reliés électriquement (fils bleus). la résistance totale est R. Ils sont placés dans un champ magnétique uniforme B. Le disque (D) tourne à la vitesse angulaire w et (D') à la vitesse angulaire w '. Calculer l'intensité du courant traversant le fil de liaison. Soit J le moment d'inertie de chaque disque par rapport à l'axe de rotation. A l'instant t=0 le disque D tourne à la vitesse angulaire w0 et D' est immobile.(frottements négligés). Exprimer w et w' en fonction du temps. Les flèches noires indiquent le sens positif de parcours du circuit. 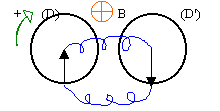Quand le disque (D) tourne de dq, le flux coupé est dF= Ba²dq/2 La fem d'induction est e = -dF/dt = Ba²/2 dq/dt =Ba²/2 w Le courant induit qui prend naissance : va mettre D' en rotation dans le même sens que D . a un sens tel que par ses effets il s'oppose à la rotation de D (i a le sens contraire au sens positif choisi de O vers M) Le disque D'coupe des lignes de champ, il y a création d'une fem induite (le courant induit va de M' vers O' ) e'= + Ba²/2 w' l'intensité du courant sera i = (e + e')/R i = Ba²/(2R) (w'-w) (w'-w)< 0, le courant a le sens contraire au sens positif de parcours. Le disque D est soumis à une force de Laplace de module F = iaB, horizontale à droite, appliquée au milieu de OM, de moment négatif : i a²B/2= B²a4/(4R) (w'-w) le th du moment cinétique s'écrit : J dw/dt= B²a4/(4R) (w-w').... (1) Le disque D' est soumis à une force de Laplace de module F=iaB, horizontale à gauche, appliquée au milieu de O'M', de moment positif: i a²B/2= B²a4/(4R) (w-w') le th du moment cinétique s'écrit : J dw'/dt= B²a4/(4R) (w-w').... (2) (1) + (2) donne : J dw/dt + J dw'/dt=0 soit w+w'=w0 = constante w'=w0-w (1) s'écrit : J dw/dt= -B²a4/(4R)(2w-w0) solution de cette équation : w = w0/2 [1+ exp( -B²a4/(4RJ))]
cours 4	courant induit dans un circuit déformable
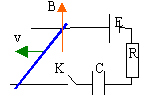
On considère 2 rails parallèles distants de l sur les quels peut glisser un un rail mobile AB de masse m. L'ensemble est placé dans un champ magnétique B uniforme. Déterminer les lois de variation avec le temps de la vitesse v et de la charge du condensateur à la fermeture de l'interupteur. Au départ AB est immobile et le condensateur n'est pas chargé. A la fermeture du circuit : le rail AB est soumis à une force de Laplace, horizontale à gauche, de module Bil. Sous l'action de cette force AB se déplace à la vitesse v. Le flux de B à travers le circuit varie et une fem e apparaît aux bornes de AB dont les effets s'opposent au déplacement de AB (e=-Blv). La loi de Pouillet s'écrit : E- Blv = Ri+Q/C.........Q charge du condensateur i=dQ/dt E- Blv = RdQ/dt + Q/C.............(1) La relation fondamentale de la dynamique s'écrit : mdv/dt= Bil d'où mdv/dt= Bl dQ/dt.............(2) l'intégration de (2) donne : v = BlQ / m repport dans (1) : RdQ/dt + Q[1/C+B²l²/m]=E l'intégration donne :
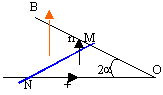
cours 5 rail mobile sur 2 rails fixes non paralèlles Le rail MN est mobile  , le triangle MNO restant isocèle. Soit r la résistance des rails par unité de longueur. Déterminer l'intensité du courant induit. Lorsque MN se déplace, le flux deB varie et une fem e apparaît aux bornes de MN . Un courant i prend naissance dont les effets s'opposent au déplacement de MN. (sens de i de N vers M) A la date t expression du flux: (OM est noté l) F= B l² sin(a)cos(a) dF/dt= 2B l dl/dt sin(a)cos(a) avec vitesse = v = dl cos(a)/dt dF/dt= 2B l sin(a) v e = -2B l sin(a) v résistance du circuit : R=r(2l+MN) = r 2l (1 + sin(a)) intensité du courant induit: i = e /R i= -Bsin(a) v / [r (1 + sin(a))] le signe négatif signifie que le courant a le sens contraire au sens positif choisi. retour - menu