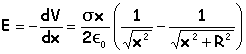révisions lycée
|
|
|
|
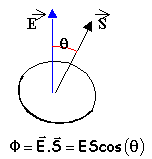
th. de Gauss Le flux du champ électrique à travers une surface fermée est égal à :
|
|||||
potentiel électrique
potentiel V en
volt
![]()
|
|
|
|
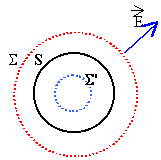 |
par raison de symétrie le champ est radial |
|
champ électrique :(point extérieur) flux envoyé à travers la sphère S de rayon r. définition du flux : F= 4pr2E th. de gauss : charge intérieure à S= charge de S =4/3 pR3r. F= 4/(3e0) pR3r E
=
R3r/(3e0r2)
Q=charge de S ; la constante est nulle (potentiel nul si r tend vers l'infini) tout ce passe comme si la charge était concentrée au centre de la sphère
E = rr/(3e0) ; potentiel : r/(2e0)(-r²/3+ R²) |
|
Calculer le champ et le potentiel crées par un cylindre infini, de rayon R, portant une densité volumique de charge r constante.
En tout point de la surface latérale S, par raison de symètrie, le champ est radial et a même module. Le flux de ce vecteur à travers la surface latérale de longueur h est E 2pxh.
En tout point de S1 ou S2 le vecteur E est normale au vecteur surface : le flux de E est nul à travers les 2 bases.
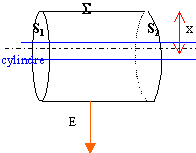
intérieure au cylindre S de rayon x :
x < r : Q=px²hr.
x >= r : Q=pr²hr.
th de Gauss :
E 2prh = Q/e0.
x < r : E= xr / (2e0)
x >= r : E= r²r / (2e0x)
potentiel électrique
![]()
si x > r : V = -r²r / (2e0) ln(x) + Cte.
Comment trouver la constante d'intégration ?
lors de la traversée de la surface du cylindre de rayon r, V est continu.
V =-r²r / (4e0) (1+2ln(x/r) )
|
|
|
|
|
|
|
|
|
|
|
 |
|
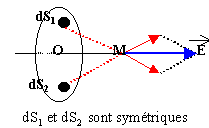
champ
le champ résultant est dirigé vers le disque si la charge est négative. |
|
|
|
|
|
|
|
|
|
|
Q=4pR²s. potentiel V = Q / (4pe0R) = Rs /e0 d'où
s =
105*8,85 10-12 /0,5
= 1,77
10-6 Cm-2
et
Q= 5,56
10-6 C
A l'intérieur d'un conducteur en équilibre le champ est nul. A la surface d'un conducteur en équilibre le champ vaut s/e0. Au voisinage, à l'extérieur de la surface d'un conducteur , le champ E est normale à la surface, a pour valeur s/e0. Il est dirigé vers la surface si les charges sont négatives et vers l'extérieur si elles sont positives. Le disque prend une charge de densité s (charge disque q = s pr²)au contact de la sphère. Ce disque est soumis à une force F colinéaire au champ et de même sens, de valeur qE= s2 pr²/(2e0) avec s= Ve0 /R F = e0pr² V²/(2R²) Le disque se soulève dés que cette force est supérieure au poids du disque( mg). d'où la valeur limite de V : V²= 2mgR² / (e0pr²) V= 425
kV
Compte tenu des dimensions du disque la charge de la sphère n'est guère modifiée. La sphère crée à cette hauteur h un champ E de valeur E= 1/ (4pe0) Q/(R+z)² = RV1 / (R+z)² Le disque atteind une position d'équilibre lorsque la force électrique s pr²E est égal au poids du disque s pr²RV1 / (R+z)²= mg avec s= V1e0 /R (R+z)²=
pe0V1²r²
/(mg)
d'où
z=0,35
m
|
|
|
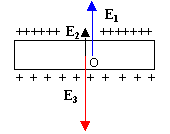
s' : densité surfacique face supérieure s'' : densité surfacique face supérieure s' s + s'' s = s s s' + s'' = s =V1e0 /R (1)
|
 |
|
E2 : du aux charges de la sphère : RV1 / (R+z)² E3 : du aux charges supérieures du disque mince : s'' /(2e0) à l'intérieur du disque , le champ est nul: (-s'' + s')/(2e0) + RV1 / (R+z)² =0 (2) résoudre le système de deux équations. s'' = 7,44 mCm-2. s'= 1,58 mCm-2. |
|