_

gaz parfait- gaz réel
cours 1	équation d'état d'un gaz parfait
Un gaz réel se comporte comme un gaz parfait à pression très faible, quelque soit la température, ou bien à basse pression et haute température. pression, volume et température sont liés : PV = nRT R = 8,31 J mol-1K-1. (constante) P : pression pascal (1 bar voisin 105 pa = 76 cm Hg ) V : volume m3 n n : quantité de matière mol T : température kelvin ( °C + 273) mélange de gaz parfaits On définit la pression partielle Pi et la fraction molaire xi du gaz dans le mélange . Pi = xi P P : pression du mélange de gaz xi = ni / n n : nombre total de moles de gaz n i : nombre de moles du gaz i masse volumique :r= m(kg)/V(m3) 1/V=P/(nRT) et n=m/ M r = MP/(RT) avec M kg mol-1. d : densité par rapport à l'air d=M/29 avec M en g mol-1 et 29 est la masse (g) d'une mole d'air. application   Une bouteille de 20 L contient du dioxygène, à la pression de 180 bars. Calculer le nombre de bouteilles de 1 L que l'on peut remplir, le gaz étant à la pression atmosphérique et à la même température. pression initiale : 1,8 107 pascals ; volume initial : 0,02 m3 ; température T Qté de matière du gaz : n=1,8 *2 105 /(RT) pression finale : 105 pascals ; volume final : V* 10-3 m3 ; température T Qté de matière du gaz : n = V*10-3 * 105 /(RT)= 100 V /(RT) 100 V = 1,8 *2 105 d'où V=3600 L auquel il faut retirer 20L : 3580 L
cours 2	gaz réel - éq. de Van der Waals
(V- nb)(P + a n²/V²) = nRT b : représente le volume propre de l'ensemble des molécules a : du fait des attractions intermoléculaires et des chocs entre les molécules, la pression réelle exercée sur chaque molécule est supérieur à P. V : volume du récipient m3 n : Qté de matière du gaz mol P : pression extérieure imposée pascal T : température K
cours 3	travail des forces de pression
Calculer le travail reçu par n moles de gaz parfait lors d'une transformation isotherme, réversible le faisant passer de l'état (P0, V0) à l'état (P1, V1). Même question pour une mole de gaz réel. Même question pour une transformation adiabatique, faisant passer une mole de l'état (P0, V0, T) à l'état (P1, V1,T1).
corrigé
isotherme: température constante PV=nRT conduit à P0V0=P1V1 travail élémentaire dW= - PdV= -nRT dV/ V=-nRT d(lnV) W = -nRT ln(V1/V0)
dW= - PdV l'équation de Wan der Waals donne P = RT/(V-b) -a dV/V² on intègre à température constante. W=-RTln((V1-b)/(V0-b) + a(1/V1-1/V0) adiabatique: pas d'échange de chaleur PVg=Cte dW= - PdV P = P0V0g /V g. dW=-P0V0g dV/V g. on intègre
cours 4	étude thermodynamique du gaz parfait
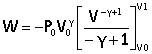
l'énergie interne U et l'enthalpie H ne dépendent que de la température dU=Cv dT .........Cv : capacité thermique à volume constant JK-1 dH=Cp dT.........Cp : capacité thermique à pression constante JK-1 Cp et Cv dépendent en général de la température Cp-Cv = nR et Cp/Cv = g (g=1,4 pour un gaz parfait diatomique, dépend de la température) (g=5/3 pour un gaz parfait monoatomique, indépendant de la température) entropie S dS=dQ/T avec dQ=Cv dT+ PdV = Cp dT- VdP application Une masse m de gaz parfait subit le cycle de transformations réversibles suivantes de A à B isobare P=105 Pa; volume V1, température T1. de B à C isochore V2=V1/5= 2L. P2= pression finale en C (Cp= 11,66 JK-1) de C à A isotherme T1=300K Calculer la pression P2, le travail et les quantités de chaleur reçue au cours du cycle corrigé état du gaz en C: P2, V2=2 L; T=300K en A : P1, V1=10 L; T=300K isotherme de C à A : P2V2=P1V1 d'où P2= 5 105 Pa travail reçu WAB =-P1DV= 105(2-10)10-3= 800 J WBC = 0 isochore dWCA = -PdV=-nRT1 dV/ V WCA =-nRT1ln( V1/V2)= -P1V1ln(5)=-105*210-3ln5= -1610 J chaleur reçue l'énergie interne ne varie pas sur le cycle W+Q=0 d'où SQ=-SW= 810 J l'énergie interne ne varie sur l'isotherme: QCA=-WCA= 1610J QAB= CpDT (isochore) = Cp(TB-T1) calcul TB: P1V2=nRTB; P1V1=nRT1 d'où TB=V2T1/V1= 60K QAB= 11,66(60-300)=-2800J 810= -2800+1610+QBC d'où QBC = 2000J
application 4	gaz parfait dans un cylindre
Un récipient indéformable, cylindrique, fermé à ses 2 extrémités est divisé en 2 parties par un piston mobile sans frottement et conducteur de la chaleur. Les parois du récipient sont imperméables à la chaleur. Les 2 compartiments contiennent de l'air,initialement: compartiment 1 : P1=2 bars; V1= 1L; T1=300K compartiment 2 : P2=1 bars; V2= 1L; T2=300K Le piston abandonné à lui même atteind une position d'équilibre. Déterminer la pression et la température finales ainsi que la variation d'entropie. corrigé n1=2105*10-3/(8,31*300)= 0,08 mol ; n2= 0,04 mol A l'équilibre, pression P et température T sont les mêmes dans chaque compatiment. Soient V'1 et V'2 les volumes finaux des compartiments. P1V1/T1 = PV'1/T et P2V2/T2 = PV'2/T et V'1+V'2=V1+V2. La variation DU d'énergie interne du gaz est nulle : parois indéformable, pas de travail reçu pas de chaleur échangée avec l'extérieur. DU=n1 Cv(T-T1) + n2Cv(T-T2)=0 T=(n1T1+ n2T2)/(n1+n2)= 300K conservation de la qté de matière du qaz n1+n2 = P1V1/(RT1) + P2V2/(RT2) = P(V'1+V'2)/(RT) P= 1,5 bars variation d'entropie dS=n(Cp dT/t - V/T dP) dS=n Cp dln(T) -nR dln(P) DS1= n1Cp ln(T/T1)- n1R ln(P/P1) calcul Cp Cp/Cv=1,4 et Cp-Cv=nR d'où Cp= nR/(1-1/1,4)=3,49 JK-1. DStotal = 0,056 JK-1.
retour - menu