_

condensateur sup
révisions lycée
cours 1	définitions et formules
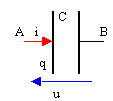
Ensemble de 2 conducteurs dont l'un entoure complètement l'autre. q=Cu ; charge ( coulomb) ; capacité C (farad F) ; u en volt énergie emmagasinée (J) = 0,5 Cu² = 0,5 q²/C E=u/e ; champ électrique entre les armatures( Vm-1) ; e : distance des armatures(m) capacité dun condensateur plan S: surface armature (m²) ; e: épaisseur isolant (m) er: permittivité relative isolant ; e0: permittivité relative du vide (8,84 10-12 Fm-1); association de condensateurs En dérivation les capacités s'ajoutent. En série localisation de l'énergie Dans toute région de l'espace où existe un champ électrique, l'énergie est localisée dans le vide avec une densité volumique 0,5e0 E²
exercice 1	trois condensateurs en dérivation
Trois condensateurs de capacité C1=1mF, C2=3,3mF, C3=4,7mF sont associés en parallèle. La charge totale du groupemenrt est q=0,216 mC. Calculer : la capacité équivalente la tension aux bornes l'énergie stockée par l'ensemble Que devient cette énergie si la tension diminue d'un tiers. corrigé Les condensateurs étant montés en dérivation, la capacité du condensateur unique équivalent à l'ensemble est C=4,7 + 1 + 3,3 =9mF. tension aux bornes u=q/C=2,16 10-4 /9 10-6 = 24V. énergie stockée :0,5 Cu²=0,5 *9 10-6 *24²= 2,59 mJ. la nouvelle tension vaut 16 V et E= 1,15 mJ.
exercice 2	associer un condensateur chargé à un condensateur non chargé
Les caractéristiques d'un condensateur sont : C=0,12 mF; e=0,2mm; er=5 ; u =100V. Calculer la surface des armatures , la charge et l'énergie emmagasinée. Ce condensateur est associé en parallèle avec un condensateur C'=0,15 mF initialement déchargé. Calculer la tension commune aux bornes l'énergie enmmagasinée par le montage. corrigé surface = C e/(e0er)=1,2 10-7*2 10-4 /(8,84 10-12*5)= 0,544 m². charge q=Cu=1,2 10-7 *100= 12mC énergie stockée : 0,5 Cu²=0,5*1,2 10-7 *104= 0,6 mJ. La charge totale n'a pas changée. capacité équivalente à l'ensemble : 0,12 + 0,15 = 0,17 m F. tension =q/C=12 10-6 /0,27 10-6 = 44,4 V. énergie 0,5*0,27 10-6*44,4²= 0,266 mJ. perte d'énergie par rayonnement électromagnétique et par effet joule dans les conducteurs lors de l'association.
exercice 3	capacité d'un condensateur sphérique
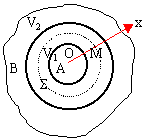
Calculer la capacité d'un condensateur dont l'armature interne est une sphère de centre O et de rayon R1. La surface interne de l'armature externe est une sphère de centre O et de rayon R2. Examiner le cas où les rayons sont peu différents R2=R1+e corrigé V1 : potentiel de l'armature interne V2 : potentiel de l'armature externe Q : charge de l'armature A Les lignes de champ sont radiales, les surfaces équipotentielles sont des sphères de centre O. Th. de gauss: calcul du champ puis du potentiel flux du champ à travers la sphère S de rayon x : E 4px²= Q/e0. E= Q/(4pe0 x²) E=-dV/dx, puisque E ne dépend que de x dV=Q/((4pe0 ) *dx/x² intégrer entre R1 et R2. V2-V1=Q/((4pe0 ) [1/R2- 1/R1] capacité = Q/(V2-V1) C= 4pe0 R1R2/(R2-R1) R2=R1+e ; e <<R1. C voisin de 4pe0 R1R2/e et 4p R1R2 surface d' une sphère C voisin de e0 S/e
exercice 4	association série 3 condensateurs
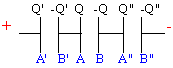
Un condensateur C est chargé sous une tension V0. On appelle A l'armature interne et B l'armature externe . C est placé en série entre 2 condensateurs C' et C" initialement non chargés. Déterminer Q, Q', Q". corrigé charges initialement l'armature A prend la charge Q0=CV0. Le conducteur AB' isolé garde la même charge :-Q'+Q=Q0. de même B et A" : -Q+Q"=-Q0. soit Q'=Q" =Q-Q0. potentiel V=VA'-VB"=Q'/C' + Q/C + Q"/C" V=(Q-Q0) (1/C'+1/C") +Q/C V=Q(1/C'+1/C+1/C")-Q0(1/C'+1/C") Q= [V+CV0(1/C'+1/C")] / (1/C'+1/C+1/C")
retour - menu - menu