_

chute libre verticale lycée
énergie mécanique
cours 1	chute libre verticale- hauteur- vitesse
Le repère d'étude est un axe vertical, orienté vers le haut. L'origine des altitudes est le sol. L'origine des temps est l'instant du lancer. altitude à la date t : z = -0,5gt² + V0t + z0 vitesse à la date t : V= -gt+V0 V² - V0² = 2g( z0-z) vitesse : ms-1 ; altitude (m) ; temps(s) ; g=9,8 ms-2 ; V0 : vitesse initiale ; z0 : altitude initiale chute libre : solide soumis uniquement à son poids
exercice 1	chute verticale vers le bas
Une bille de masse m=10g est lachée sans vitesse d'une hauteur de 50 m. Calculer : la vitesse atteinte et la distance parcourue à t=2s. la durée de la chute et la vitesse d'arrivée au sol. l'énergie potentielle initiale. (origine des altitudes : le sol) Si la masse double que deviennent les résultats précédents. corrigé altitude initiale z0=50 m ; V0=0 à t=2 s : z=-4,9 *2² + 50 = 30,4 m ; distance parcourue : 19,6 m vitesse algébrique=-9,8*2=-19,6 ms-1=-19,6*3,6 kmh-1 le signe moins signifie que le vecteur vitesse est dirigé vers le bas alors que l'axe des altitudes est dirigé vers le haut. norme du vecteur vitesse : 19,6 ms-1. arrivée au sol z=0 ; -4,9 t²+50=0 ; t =rac carrée(50/4,9 )= 3,19 s norme de la vitesse = val absolue(-9,8*3,19) = 31,3 ms-1. énergie potentielle de pesanteur = mgz =0,01*9,8*50 = 4,9 J vitesse, durée et distance sont indépendantes de la masse seule l'énergie potentielle double.
exercice 2	chute libre verticale (plus dur)
La distance parcourue durant la dernière seconde de chute libre(sans vitesse initiale) est égale au quart de la distance totale de chute. Quelle est la hauteur de chute ? Une bille est abandonnée sans vitesse initiale . Quelle est la distance parcourue pendant la neme secondes de chute ? g=10ms-2 corrigé distance parcourue = d = z0-z = 4,9 t² (t durée de la chute) 0,75 d= 4,9 (t-1)² diviser membre à membre la seconde relation par la pemière : 0,866 t=t-1 d'où t= 7,46 s. distance parcourue d= 4,9*7,46²= 272,8 m t=1s alors x =5 m t=2s alors x=20 m soit 15 m durant la 2éme seconde soit 5*(2n-1) avec n=2 t=3 s alors x=45 m soit 25 m surant la 3éme seconde soit 5*(2n-1) avec n=3
exercice 3	lancer vertical de 2 balles
Une première balle est lancée vers le haut avec une vitesse initiale de 8 ms-1 . Une seconde plus tard une autre balle est lancée vers le haut avec une vitesse initiale de 6 ms-1. Les deux balles partent du même endroit choisi comme origine. Quelle est l'altitude de la rencontre ? corrigé origine des temps : départ de la 1ère balle balle n°1 : z = -4,9 t² + 8t balle n°1 : z = -4,9 (t-1)² + 6(t-1) La 1ère balle commence à redescendre lorsque la 2ème la rencontre. -4,9 t² + 8t = -4,9 (t-1)² + 6(t-1) développer t = 10,9 / 7,8 = 1,4 s. altitude : -4,9 *1,4² + 8 *1,4 = 1,6 m
exercice 4	profondeur du puits
On lache une pierre sans vitesse du haut d'un puits. On entend "plouf" 3 s après le lacher. Quelle est la profondeur du puits ? vitesse du son dans l'air 340 ms-1. corrigé t1 durée de la chute et t2 durée de la remontée du son d : profondeur du puits t1 + t2 = 3 (1) chute libre : d = 4,9 t1² son : d = 340 t2 4,9 t1²= 340 t2 (2) 4,9t1²=340 (3-t1 ) développer et résoudre t1= 2,88 s profondeur 340*0,12 = 40,7 m
exercice 5	parabole
On lance un objet avec une vitesse initiale de 21,2 m/s dans une direction faisant un angle de 45° avec l'horizontale. S'il n'y avait pas de pesanteur, le principe d'inertie s'appliquerait. Quel serait alors le mouvement de l'objet? Repésenter les positions de l'objet au bout de 1, 2, 3 s. Echelle : 1cm pour 10 m. Sous l'action de la gravité, l'objet se retrouve plus bas que la trajectoire trouvée, d'une distance donnée par la loi de la chute libre. Placer les positions réellement atteintes au bout de 1, 2, 3 s. Au bout de combien de temps l'objet touche t-il le sol supposé horizontal? Peut-on en déduire la vitesse horizontale qu'il avait au moment du lancer? g=10 N /kg. corrigé absence de pesanteur: le solide n'est soumis à aucune force ( solide isolé) alors le mouvement de son centre d'inertie dans un référentiel galiléen est rectiligne uniforme.( droite confondue avec la vitesse initiale inclinée de 45° sur l'horizontale) distance (m) = 21,2 * temps en seconde. 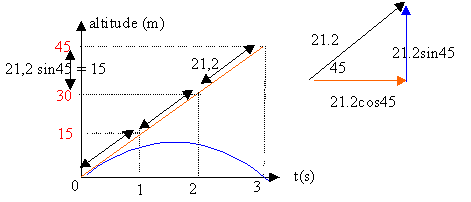présence de la pesanteur : ( force verticale) seule la composante verticale de la vitesse est modifiée alors que la composante horizontale de la vitesse reste inchangée.   loi de la chute libre avec vitesse initiale : altitude (m) = -5 *temps ² +21,2 sin (45°) *temps (le temps est en seconde) le signe moins vient du fait que dans le repère choisi l'axe des y est vertical vers le haut alors que g ( gravité) est vertical vers le bas. h = - 5t² +15 t t = 1s : h = -5 +15 = 10 m t= 2 s : h = -5*4 +30 = 10 m t=3 s : h = -5 *3² + 45 = 0 m ( on est au sol)   ou bien plus simplement : écart entre la droite et la parabole : 5 t² soit ( 5*1² ; 5*2²=20; 5*3²=45) composante horizontale de la vitesse au moment du lancer : à t =3 s l'objet est au sol x = composante horizontale de la vitesse * temps le mouvement suivant l'axe des abscisses est rectiligne uniforme car il n'y a aucune force dirigée suivant l'horizontale composnte horizontale de la vitesse : 21,2 cos45=15 m/s retour - menu - menu