|
|
|
|
notations usuelles
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
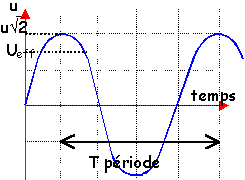
On représente une grandeur sinusoïdale par
- un vecteur de norme U formant l'angle Y avec l'axe horizontal .
- un nombre complexe de module U, d'argument Y. (j²=-1)
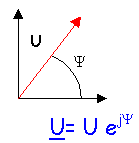
|
|
||
|
|
|
|
|
|
||
|
de valeur efficace Uw |
de valeur efficace U /w |
|
|
|
|
|
|
|
|
|
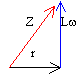
impédances Z ohm ; admitance Y=1/Z
|
|
notation |
|
|
|
|
|
|
|
|
|
||
|
|
 |
|
|
||
|
|
 |
|
|
Danger !!!!! ces mêmes lois ne s'appliquent pas ni aux grandeurs efficaces , ni aux grandeurs instantanées
|
|
|
|
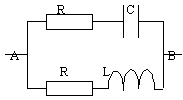
exemple de calcul d'une impédance complexe
- l'impédance complexe
- l'impédance réelle
- la phase de U par rapport à celle de I prise comme origine
..
contrôler constamment l'homogénéité des calculs ,
en se souvenant que LCp² est sans dimension ,
et que L/C est le carré
d'une impédance.
impédance complexe Z1=R+1/(pC) Z2=
R+pL Z1Z2 /
(Z1+Z2)
(R+1/(pC))(R+pL)/(2R+pL+1/(pC))
(R²+L/C+R(Lp+1/(pC)) / (2R+pL+1/(pC))
or(Lp+1/(pC) =0 dans cet exercice
Z= (R²+L/C)/ (2R) grandeur réelle ,
donc tension aux bornes du dipole et intensité principale en phase
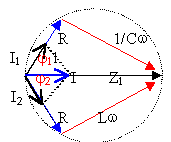
exercice précédent : calculs des intensités
calculer la pulsation dans le cas où LCw²=1 déterminer les intensités dans chaque branche, l'intensité principale.
.
|
|
|
 |
|
Z1=111,8 W |
Z2=111,8 W |
|
|
tan(j1)=Lw/R=100/50=2 j1= 63,4° |
j2= -63,4° |
 |
|
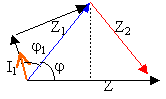
2*I1cos(j1) ou UAB/Z 2*0,089*cos63,4= 0,079A |
=62,5/111,8=0,559 j= 56° |
puissance active watt, réactive var, apparente VA
|
|
|
|
|
|
|
|
|
|
|
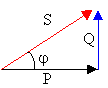
Q et S intermédiaires commodes de calcul, mais pas de sens physique
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
conservation des puissances à la traversée d'un dipôle
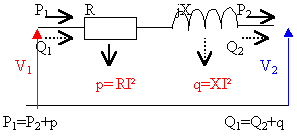
schéma parallèle équivalent à une bobine
.
|
|
|
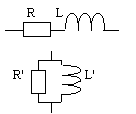 |
|
1/Z=1/(R+pL) 1/Z=(R-pL) /(R²-p²L²) |
|
|
|
|
L'=(R²+L²w²)/(L²w²) |
|
w=2pf=6,28*8 104=5,024 105 rads-1.
Lw= 7536 ; (Lw)²=5,68 107.
R'=450kW ; L'=15,3 mH
relevement du facteur de puissance
|
j déphasage courant tension |
 |
|
|
|
relevement du facteur de puissance
- l'impédance, le facteur de puissance.
- les puissances active, réactive et apparente.
- On désire que la puissance réactive consommée par le circuit soit nulle. On utilise un condensateur supplémentaire C' . Comment brancher C' et C? Calculer la capacité C'.
.
w=2pf=6,28*100= 628 rads-1.
Lw = 0,2*628= 125,6 W; 1/Cw=1/(4 10-6*628)=398 W.
(Lw-1/Cw)²=7,4 104 ; R²=4 104; Z= 337 W .
cos(j)=R/Z= 200/337= 0,593
Danger!!!! .... deux solutions pour j +53,6 ou -53,6
1/Cw
est supérieur à Lw
donc j
=-53,6
intensité efficace
=U/Z=20/337= 0,0593 A
P=UIcos(j)= 20*0,0593*0,593= 0,703 watt
P=UIsin(j)=20*0,0593*(-0,805)= -0,984 vars
S=UI
= 20*0,0593
= 1,186
VA
La puissance réactive est nulle si la
réactance du dipole est nulle. Soit C1 la
capacité équivalente aux
condensateurs.
Lw-1/C1w=0 ou C1=1/(Lw²)= 1,267 10-5 F
A partir de 4 mF il faut associer 8,67 mF en dérivation pour obtenir 12,6 mF
études graphiques -facteur de puissance.
|
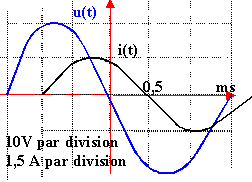 |
..
intensité efficace = 1,5/1.414 = 1,06 A
fréquence =1/0,003= 333,3 Hz
w=2pf=6,28*333,3= 2093 rad s-1.
tension en avance sur intensité (donc bobine inductive ) de 1/6 période ou p/3 rad
cos(j)=
0,5
puissance active
UIcos(j)=
14,14*1,06*0,5= 7,5
W
puissance réactive UIsin(j)= 14,14*1,06*0,866= 13 vars
puissance apparente
UI=
14,14*1,06= 15 VA
résistance de la bobine
:P=rI²=7,5
r=7,5/1,06²= 6,7 W.
inductance de la bobine :Q=LwI²=13
L=13/(1,06²*2093)=
5,5 mH
le facteur de puissance doit
être égal à
cosj
= 0,9
sinj = 0,436 et Q=14,14*1,06*0,436 = 6,54 vars
Q=(Lw-1/Cw)I² d'où C = 83mF
retour - menu - menu