pHmétrie, conductimétrie, spectrophotométrie
Dosage d' une solution d'ammoniac (pKa = 9,2) de concentration cb=0,01 mol/L par une solution d'acide chlorhydrique de concentration ca=0,01 mol/L. A un volume vb=10 mL de solution d'ammoniac on ajoute un volume V0 = 100 mL d'eau. On ajoute à ce mélange, un volume v d'acide à l'aide d'une burette.
- Etablir l'équation de la courbe de dosage pH=f(v) au voisinage de la demi-équivalence.
- Etudier la dérivée dpH/dv et conclure.
corrigé
Dans la solution d'ammoniac (NH3), la seule réaction pouvant se produire est :
NH3+H2O=NH4++HO-.
constante de réaction : K1 = [NH4+][HO-] / [NH3] = [HO-][H3O+] [NH4+] / ([NH3] [H3O+] )=10-14 / 10-9,2 = 10-4,8.
la réaction de l'ammoniac avec l'eau est très limitée et l'espèce majoritaire dans la solution d'ammoniac est NH3.
La réaction du dosage est :
NH3+H3O+= NH4++H2O
constante de cette réaction : K= [NH4+] / ([NH3] [H3O+] ) = 1 / 10-9,2 = 109,2.
cette constante étant très grande, la réaction du dosage est totale.
A l'équivalence les quantités de matière des réactifs sont dans des proportions stoechiométriques
Qté de matière de base : cb vb = 0,01*10-2 = 10-4 mol
Qté de matière d'acide : ca va éq= 0,01 va éq = 10-4 soit va éq= 10 mL
A la demi-équivalence on a donc introduit 5 mL d'acide chlorhydrique. La réaction du dosage étant totale, la quantité d'ion oxonium ajouté est donc égale à la quantité d'ion ammonium formé :
[NH4+] = ca v / (V0+vb+v)
il reste : [NH3] = (cb vb -ca v )/ (V0+vb+v)=(ca va éq-ca v )/ (V0+vb+v) = ca(va éq-v )/ (V0+vb+v)
la constante d'acidité du couple NH4+/NH3 s'écrit : Ka= [NH3] [H3O+] /[NH4+]
Ka=(va éq-v )[H3O+] / v ; log Ka= log [H3O+] + log ((va éq-v )/v)
pKa = pH-log ((va éq-v )/v) ; pH= pKa +log ((va éq-v )/v).
calcul de la dérivée dpH /dv:
dérivée de log u : u'/u avec u = (va éq-v )/v et u'= -(va éq / v²)
dpH /dv = -va éq / ((va éq-v )v).
au voisinage de la demi-équivalence dpH/dv présente un minimum
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Une solution de soude de concentration initiale c1, laissée à l'air libre, dissout le CO2 atmosphérique. Soit c2 la concentration de CO2 dissout par litre de solution. On dose un volume vb=10 mL de la solution de soude carbonatée par V ml d'acide chlorhydrique (ca=0,1 mol/L) en présence de phénolphtaléine. L'indicateur change de couleur pour V1=16 mL. On ajoute un peu d'hélianthine et le dosage se poursuit : un deuxième virage est observé pour V2=20 mL
couples acide base CO2(aq) /HCO3- pKa1=6,3 ; HCO3-/CO32- : pKa2=10,3 ;
zône de virage : hélianthine [3,1 ; 4,4 ] ; phénolphtaléine [8 ; 9,9]
- Quelles sont les espèces majoritaires avant le
début du dosage ?
- Exprimer leurs concentrations en fonction de c1 et c2. - Ecrire les équations de dosage lors des deux étapes.
- Déterminer c1 et c2.
- Pour quelle valeur du volume V le pH vaut-il 10,3 ?
corrigé
La dissolution du gaz carbonique de l'air est suivie de la réaction :
CO2(aq) + HO- = HCO3-
avec K= [HCO3- ] / ([CO2(aq)][HO- ])= [HCO3- ][H3O+] / ([CO2(aq)][HO- ][H3O+])= 10-6,3 / 10-14 =107,7.
cette réaction est totale.
La réaction suivante se produit alors :
HCO3- + HO- = CO32- +H2O
avec K= [CO32- ] / ([HCO3-][HO- ])= [CO32- ][H3O+] / ([HCO3-][HO- ][H3O+])= 10-10,3 / 10-14 =103,7.
cette réaction est totale, sauf si la solution de soude a dissout une quantité importante de CO2 soit (c2<c1)
Or la différence entre V2 et V1 est faible donc c2<c1)
espèces présentes initialement en solution :
Na+ ( ion spectateur) tel que [Na+]=c1 ; [CO32- ] = c2 ; [HO- ] = c1-c2 ;
lorsque V=V1 mL d'acide ajouté, le pH est compris entre 8 et 9,9 , un peu inférieur à pKa2 : les ion hydroxyde et carbonate ont réagi avec l'ion oxonium suivant :
H3O+ + HO- = 2 H2O (1)
H3O+ + CO32- = HCO3-+ H2O (2)
à l'équivalence : caV1 = (c1+c2 )vb.
En poursuivant le dosage ( en présence d'hélianthine) on dose l'ion hydrogénocarbonate.
HCO3-+ H3O+ =CO2(aq)+2 H2O (3)
à l'équivalence : ca(V2-V1)= c2 vb.
c2 = 0,04 mol/L et c1 = 0,12 mol/L.
Si pH=10,3=pKa2 alors [HCO3-]=[CO32- ] ; tous les ions HO- sont dosés ; la moitié des ions carbonate CO32- sont dosés:
Qté d'acide versé : ca V = (c1 +½ c2 )vb soit V= (0,12+0,02)*10/0,1= 14 mL.
Un volume va d'une solution d'acide chlorhydrique de concentration ca est dosée par une solution de soude de concentration cb. On ajoute V0 mL d'eau ; la soude est versée à l'aide de la burette et le dosage est suivi par conductimétrie.
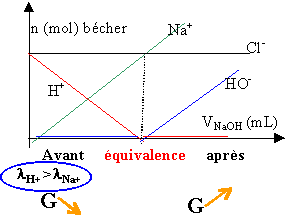
- Tracer la courbe donnant la conductivité de la solution en fonction du volume v de soude versé. Interpréter.
ca=cb=0,01 mol/L ; va=10 mL ; v0=100 mL
conductivité équivalente limite ( Sm² mol-1) : lNa+ = 5 10-3 ; lCl- = 7,63 10-3 ;lH3O+ = 39,48 10-3 ;lHO- = 19,85 10-3 ;
corrigé
Inventaire des ions : ions chlorure et sodium : soit v le volume de soude ajouté.
[Cl-]= cava / (va+v0+v) ; [Na+]= cbv / (va+v0+v) ;
La solution demeure électriquement neutre : [H3O+]+[Na+] = [HO-]+[Cl-]
pour v <vequi , le milieu est acide et [HO-] est négligeable devant [H3O+]
[H3O+] = [Cl-] -[Na+] = (cava-cbv)/(va+v0+v)
conductivité de la solution : s = lNa+ [Na+] +lCl- [Cl-] +lH3O+ [H3O+]
s = [lNa+ cbv +lCl-cava +lH3O+(cava-cbv)]/(va+v0+v)
s = [(lNa+ -lH3O+)cbv +(lCl-+ lH3O+) cava ]/(va+v0+v)
Si le volume total de la solution varie très peu, c'est l'équation d'une droite de coefficient directeur :
(lNa+ -lH3O+)cb /(va+v0) = (5-39,48) 10-3 * 10 / (110 10-6) = -3134.
cb= 0,01 mol/L= 10 mol/m3et volume en m3.
pour v >vequi , le milieu est basique et [H3O+] est négligeable devant [HO-]
[HO-] = [Na+] -[Cl-] = (cbv-cava)/(va+v0+v)
conductivité de la solution : s = lNa+ [Na+] +lCl- [Cl-] +lHO- [HO-]
s = [lNa+ cbv +lCl-cava +lHO-(cbv-cava)]/(va+v0+v)
s = [(lNa+ +lHO-)cbv +(lCl-- lHO-) cava ]/(va+v0+v)
Si le volume total de la solution varie très peu, c'est l'équation d'une droite de coefficient directeur :
(lNa+ +lHO-)cb /(va+v0) = (5+19,85) 10-3 * 10 / (110 10-6) = +2259.
cb= 0,01 mol/L= 10 mol/m3et volume en m3.
Un indicateur coloré contient un couple acide base noté Hin / In- de constante d'acidité Ka. On note c la concentration de l'indicateur coloré, ea et eb les coefficients d'absorption molaires respectivement de la forme acide et de la forme basique à la longueur d'onde lmax.
- Exprimer l'absorbance totale A à la longueur
d'onde lmax, en
fonction de [HIn], [In-],
ea et eb
ainsi que de la longueur L de la cuve.
- Quelle est la valeur Amax de A en milieu très acide ?
- Quelle est la valeur Amin de A en milieu très basique ? - Quelle relation existe-t-il entre Amax ,
Amin , A, Ka et
[H3O+] ? Pour le rouge de
méthyl à 530 nm, les mesures
effectuées sont rassemblées dans le tableau
ci-dessous :
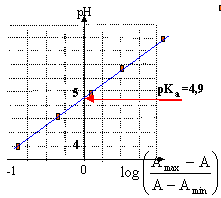
- Calculer le pKa du couple Hin / In- .pH 3 3,2 4 4,6 5 5,4 6 7 7,3 A 2 2 1,78 1,4 0,92 0,48 0,16 0 0
corrigé
L'absorbance d'une solution est la somme des absorbances des ions et des molécules de cette solution : A= SeiLci .
A= L(ea [HIn] + eb [In-])
en milieu très acide [In-] proche de zéro et en conséquence [HIn] proche de c et Amax = Lea c.
en milieu très basique [HIn] voisin de zéro et donc [In-] voisin de c et Amin = Leb c.
conservation de la matière d'indicateur coloré : [HIn] + [In-] = c
Amax-A = L[ ea c- (ea [HIn] + eb [In-])]=L[ ea ( c- [HIn] )- eb [In-])] = L[ ea [In-] - eb [In-])]
Amax-A = L (ea - eb )[In-] soit [In-] = (Amax-A)/(L (ea - eb ))
de la même manière :
Amin-A = L[ eb c- (ea [HIn] + eb [In-])]=L[ eb ( c- [In-] )- ea[HIn] )] = L[ eb [HIn] - ea [HIn] )]
Amin-A = L (eb - ea )[HIn] ; [HIn] = (A-Amin) / (L (ea - eb )).
Or pH=pKa + log ( [In-] / [HIn] )
d'où pH= pKa + log ((Amax-A)/ (A-Amin)).
tracer la droite d'équation pH= f( log ((Amax-A)/ (A-Amin))), de pente égale à un et dont l'ordonnée à l'origine vaut pKa.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La phénantroline donne avec l'ion Fe2+ un complexe de couleur rouge utilisé comme indicateur coloré redox. La réaction de formation du complexe est : Fe2+ + n phen = Fe (phen)n2+. But : déterminer la valeur de n.
Une solution contient initialement les concentration [Fe2+]0 en ion fer II et [phen]0 en phénantroline. On pose c0 = [Fe2+]0 +[phen]0 et X= [phen]/ c0. On mesure l'absorbance A de différents mélanges ayant tous la même concentration initiale. Seuls les ions fer II et le complexe absorbent à la longueur d'onde l considérée. On note e1 et e2 les coefficients d'absorption molaires respectivement de l'ion fer II et de la forme complexe à la longueur d'onde l. La longueur de la cuve est notée L.
- Exprimer l'absorbance A des mélanges en fonction des concentrations à l'équilibre [Fe2+] et [phen].
- Soit Xs la valeur de X lorsque les réactifs sont en proportions stoéchiométriques. Exprimer Xs en fonction de n.
- La réaction de formation du complexe est
quantitative ; établir l'expression
Y=A-A0 en fonction de X où
A0 représente l'absorbance du
mélange s'il n'y avait pas de réaction. Il
faudra distinguer deux cas X<Xs et
X>Xs.
- Quelle est l'expression de Y pour X=Xs ?
- Comment peut-on obtenir n à partir de la courbe Y=f(X) ? Les valeurs de Y ont été déterminées expérimentalement à l =500 nm pour c0 = 8 10-4 mol/L.
- Déterminer la valeur de n.X 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 Y 0,2 0,46 0,72 0,98 1,2 1,46 1,73 1,44 0,72 0,01
corrigé
L'absorbance d'une solution est la somme des absorbances des ions et des molécules de cette solution : A= SeiLci .
A= L(e1 [Fe2+] + e2 [Fe (phen)n2+])
Si les réactifs sont en proportions stoechiométriques alors : n [Fe2+]0 = [phen]0 .
c0 = [Fe2+]0 +[phen]0 = [Fe2+]0 +n [Fe2+]0 = (n+1)[Fe2+]0
or Xs= [phen]0 / c0 d'où : Xs= n [Fe2+]0 / ((n+1)[Fe2+]0 ) = n / (n+1).
En l'absence de réaction : A0 = L(e1 [Fe2+] 0.
Y=A-A0 = L(e1 ([Fe2+] -[Fe2+] 0)+ e2 [Fe (phen)n2+])
phénantroline en défaut : X<Xs.
[Fe (phen)n2+] = [phen]0 /n = c0X / n
conservation de l'élément fer : [Fe2+]+[Fe (phen)n2+] = [Fe2+] 0.
soit [Fe2+]-[Fe2+] 0 = -c0X / n d'où Y= L(-e1 c0X / n + e2 c0X / n ) = L c0X / n (e2 - e1 ).
ion fer II en défaut : X>Xs.
[Fe (phen)n2+] = [Fe2+]0.
or c0 = [Fe2+]0 +[phen]0 =[Fe (phen)n2+] +c0X
d'où : [Fe (phen)n2+] = c0 (1-X) et Y= L c0(1-X)(e2-e1).
si X=Xs, il n'y a plus à l'équilibre ni ion fer II ni phénantroline : dans l'une ou l'autre des expressions de Y, remplacer alors X par Xs=n/(n+1)
d'où Y= L c0(e2-e1)/(n+1)
la courbe Y=f(X) est constituée de deux demi-droites de pentes L c0 / n (e2 - e1 ) et -L c0(e2-e1).
Le rapport des deux pentes -7,2 et 2,4 donne la valeur de n. les coordonnées du point d'intersections donne également la valeur de n. n =3.
retour - menu